Все цифровое оборудование, от самого простейшего до сложного, сконструировано и изготовлено с использованием относительно малого количества основных схем. Все эти схемы, которые называются логическими элементами, выполняют некоторые элементарные логические функции с двоичными данными.
Логические схемы делятся на два основных типа: память и схемы принятия решений. Для хранения двоичных данных используются схемы памяти. Логические схемы принятия решений отслеживают двоичные сигналы на входах и выдают выходной сигнал, основанный на состояниях входных сигналов и характеристиках самой логической схемы.
Логический элемент на схемах изображают прямоугольником. Линии, которые находятся с левой стороны этого прямоугольника называются входами, а с правой — выходами элемента. Внутри самого прямоугольника изображен указатель логической функции, которую выполняет данный элемент. Такими указателями могут быть различные значки; иногда ими служат слова-связки, присутствующие в логических высказываниях. Это известные нам не, или, а также и.
Предложение со словом не (английское no) называется отрицанием первоначального предложения. Функцию отрицания в электронике выполняет логический элемент НЕ — инвертор. Инвертор имеет один вход и один выход и устроен так, что если подать на его вход потенциал, соответствующий единице, то на его выходе будет потенциал, соответсвующий нулю.
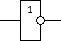
| Потенциал на входе | Потенциал на выходе |
| 0 | 1 |
| 1 | 0 |
Слово или (or) служит для связки двух простых предложений в сложное. Такая связка в логике называется дизъюнкцией или логическим сложением. Логический злемент ИЛИ называют дизъюнктором. Он имеет два входа.
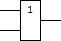
| Потенциал на входе | Потенциал на выходе | |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Слово и (and) применяется для соединения двух простых предложений в сложное. Называется это соединение конъюнкцией. Конъюнктор (логический элемент И) тоже имеет два входа.
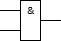
| Потенциал на входе | Потенциал на выходе | |
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Помимо указанных логических элементов существует еще множество их, которые выполняют более сложные логические операции. Эти операции являются комбинациями вышеперечисленных простейших логических преобразований. К числу таких элементов относятся, например, элементы ИЛИ-НЕ, И-НЕ, И-ИЛИ-НЕ.
Для того, чтобы построить логическую схему, необходимо произвести следующие действия. Во-первых, построить таблицу истинности данного проектируемого узла по исходным условиям работы, т.е. по соответствию его входных и выходных сигналов. Во-вторых, по этой таблице записать формулу логической функции этого узла, а затем произвести минимизацию (если это необходимо) данной формулы. Наконец, в-третьих, построить логическую схему узла.