Линейным называется алгоритм, в котором все этапы решения задачи выполняются строго последовательно. Структура такого алгоритма показана на рисунке:

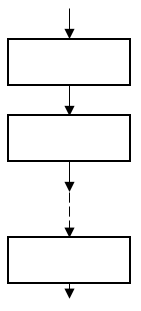
Рассмотрим пример.

Задача 1. Даны переменные А и Б. Требуется обменять их значения, т. е. переменная А должна получить значение Б, а Б — значение А.

Решение.

1. Исходные данные: А, Б. Результат: А, Б.

2. Метод решения задачи:

В ЭВМ каждая величина хранится в отдельной ячейке. Поэтому задача фактически заключается в том, чтобы поменять местами содержимое двух ячеек. Задача аналогична такой «жизненной» ситуации. Имеются две клетки — в одной находится волк, в другой — заяц. Требуется поменять их местами, т. е. пересадить их из одной клетки в другую.

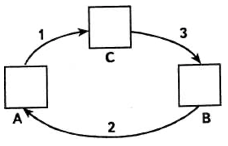
Введем в рассмотрение еще одну величину, например С, т. е. выделим третью ячейку (клетку), свободную; перенесем значение А в ячейку для С (С := А), затем перенесем значение Б в ячейку для А и т. д. (на рисунке ячейки изображены квадратиками, операции — стрелками, порядок выполнения операций — цифрами).

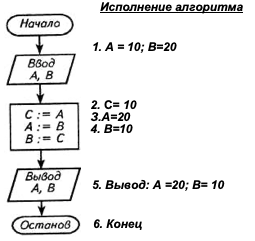
Решение задачи распадается на три этапа. Соответствующие им блоки и порядок их выполнения изображены на схеме алгоритма, показанного ниже. Для отладки исполним его, взяв в качестве теста такие данные: А = 10, Б = 20. Результаты исполнения приведены на том же рисунке. Сравнение их с исходными данными задачи свидетельствует о том, что алгоритм работает верно.

Задача 2. Даны величины А, В, С, D. Требуется переместить значения величин: В должно получить значение А; С — значение В; D — значение С.

Решение.

1. Исходные данные А, B, С, D. Результат: А, B, С, D.

2. Метод решения задачи: сразу приходит в голову следующая последовательность действий:

В := А

С := В

D := C.

Для отладки исполним ее, взяв в качестве теста такие значения величин: А = 5; Б = 10; С = 20; D = 100.

Результаты исполнения:

1) Б = А = 5; 2) С = B = 5; 3) D = C = 5.

Результаты говорят о том, что алгоритм неверен — перемещения значения величин не произошло. Следует, очевидно, те же операции выполнять в обратном порядке, как показано на рисунке:

В соответствии с этим рисунком, изобразим схему алгоритма:

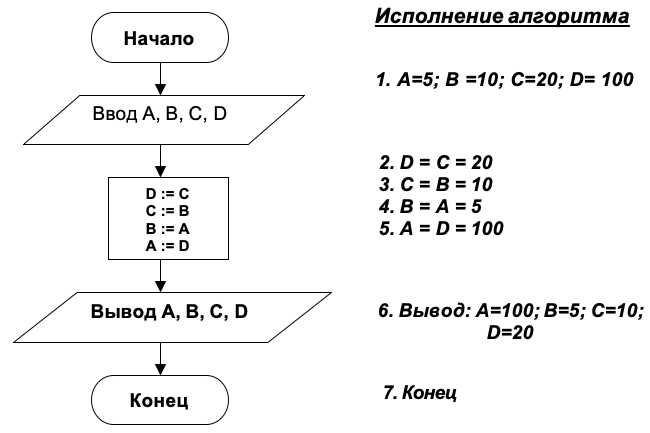
В результате выполнения операции D := С величина D получает новое значение, при этом прежнее значение D стирается. После операции В := А величина В получает новое значение, при этом величина А свое значение сохраняет, поскольку ей не присваивалось другое значение — любая величина сохраняет свое значение, пока ей не будет присвоено новое, т.е. чтение числа из ячейки памяти не изменяет содержимого ячейки.

Исполнение алгоритма при принятых выше значениях исходных величин подтверждает, что алгоритм верен.