Порядок составления их определяется Основными принципами алгоритмизации. Эти принципы можно дополнить еще одним: в сложных задачах выделяются в первую очередь наиболее крупные этапы решения задачи (подзадачи) и изображается порядок выполнения их в виде схемы, называемой укрупненной. Далее каждая подзадача рассматривается отдельно как самостоятельная задача и для каждой составляется своя схема алгоритма. Только после этого составляется подробная схема алгоритма всей задачи совмещением схем отдельных подзадач.

Задача. Задан массив B(1:4). Каждому элементу массива присвоить значение соседнего с ним справа. Последнему элементу присвоить значение первого.

К этой задаче сводится, например, следующая: в списке учащихся первую по списку фамилию поставить на последнее место. В результате второй элемент списка станет первым, третий элемент — вторым, четвертый — третьим, и т. д. Здесь список можно рассматривать как одномерный текстовый массив.

Решение.

Исходные данные:

массив B(1:4) = {b₁, b₂, b₃, b₄}

Результат:

массив В(1:4)

Пояснение. Иногда некоторые считают, что результатом должен быть другой массив, не совпадающий с исходным. Но это не так! Как отмечалось, для каждого элемента массива выделяется отдельная ячейка памяти ЭВМ. Новый массив потребует новых ячеек. В нашем случае новые ячейки не требуются, так как здесь меняется только содержимое исходных ячеек, поэтому результатом будет тот же массив B(1:4).

Для нашей задачи, можно подобрать аналогичную «жизненную» ситуацию. Например, имеются четыре клетки с кроликами, расположенные в ряд. В каждой клетке один кролик. Требуется пересадить каждое животное в соседнюю слева клетку, а из первой клетки пересадить в последнюю. Размеры клетки не позволяют помещать в одну клетку более одного кролика:

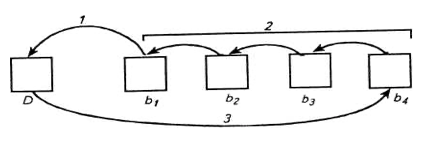
Порядок решения этой задачи ясен. По аналогии с ним можно сформулировать и метод решения нашей задачи со всеми подробностями, но предварительно запишем «план» ее решения.

1. Очевидно, потребуется свободная ячейка (клетка). Поэтому введем в рассмотрение некоторую величину D и первой операцией будет такая: D := b₁, т. е. значение b₁ перенесем в свободную ячейку.

2. Значения элементов b₂ — b₄ переносим на место элементов b₁ — b₃ соответственно.

3. Последняя операция — перенесем значение b₁ в ячейку для b₄ т. е. b₄ := D.

Изобразим теперь план решения в виде схемы алгоритма. Это и будет укрупненная схема алгоритма задачи. Она отражает суть нашей задачи — составляющие ее подзадачи и порядок их решения:

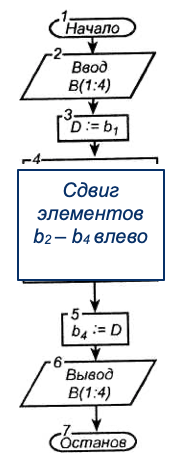
Далее для каждой подзадачи отдельно составим схему алгоритма ее решения. Однако в этом нуждается задача только 4-го блока (блоки, подобные блоку 4, называются укрупненными; они имеют особое обозначение на схеме алгоритма):

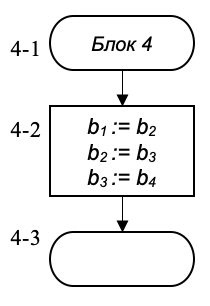
В блоке 4-1 вместо слова Начало записано Блок 4. И впредь схему алгоритма, раскрывающую некоторый укрупненный блок, будем начинать с имени этого блока; последний блок такой схемы оставляем незаполненным, так как здесь он обозначает не прекращение вычислений, а завершение некоторого участка схемы алгоритма. Далее объединяем схему алгоритма решения всей задачи со схемой укрупненного блока 4. В результате получим подробную схему всей задачи:

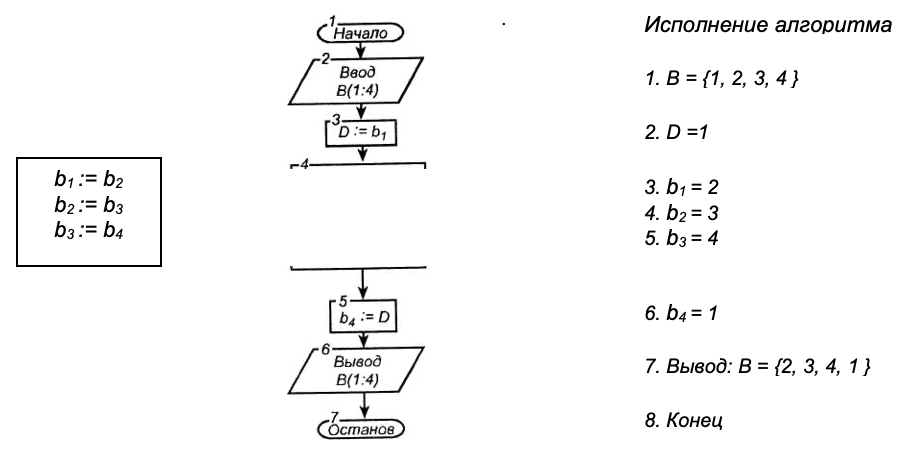
Для отладки алгоритма задачи исполним его, приняв в качестве тестового набора такие значения элементов массива В(1:4) = {b₁, b₂, b₃, b₄} = {1, 2, 3, 4}.

Анализ результатов работы алгоритма говорит о том, что алгоритм правильно решает задачу.

Задача. В обувной магазин поступила партия обуви различных размеров и разной цены. Данные представлены в таблице ниже. Определить стоимость всей партии обуви после повышения цен на обувь в N раз и новые цены.

Размеры обуви	Количество пар	Цена одной пары, тыс. руб.
38 39 41	120 50 93	3 4 9

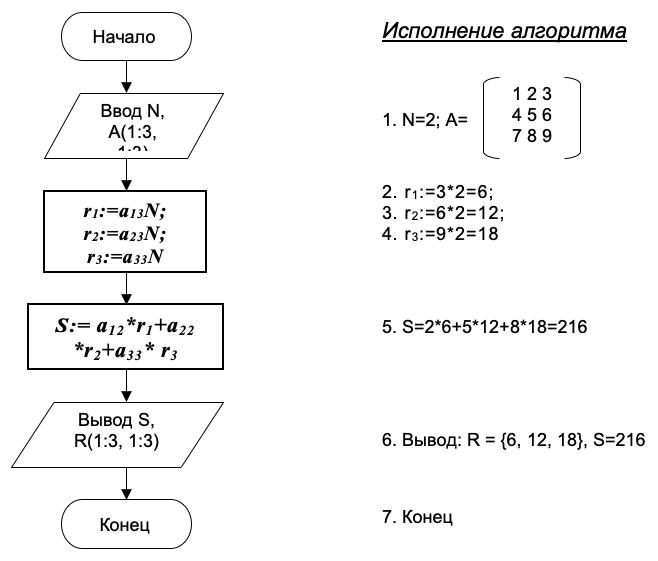
Решение. Очевидно, при работе с данными таблицы потребуются обозначения (имена) для ее элементов. Поэтому естественно представить их как двумерный массив (матрицу) А(1:3, 1:3):

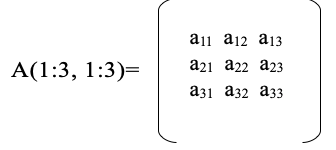
Результаты можно представить в виде массива R(1:3) — новые цены, и переменной S — стоимость всей партии обуви.

Теперь, задачу можно сформулировать математически: задана матрица А(1:3, 1:3); умножить элементы третьего столбца этой матрицы на N (образовать массив R(1:3)) и вычислить значение S по формуле:

S = a₁₂ * r₁ + a₂₂ * r₂ + a₃₂ * r₃

Пояснение. Формулировка задачи неоднозначна (это типично для реальных задач) — результаты умножения на величину N допускают различные представления:

— можно записать их на место исходных элементов в массив А;

— можно организовать из них новый массив, как мы и поступили, руководствуясь соображением — не следует без необходимости искажать исходные данные.

Метод решения задачи (в общем виде) (план решения задачи):

1) умножение элементов третьего столбца матрицы А на N и образование массива R(l:3);

2) вычисление S по формуле (см. выше). Соответствующая укрупненная схема алгоритма изображена на рисунке:

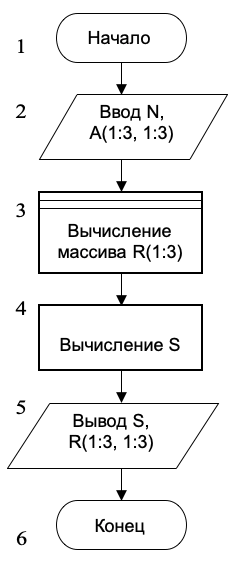
Теперь по отдельности рассмотрим операции блоков 3 и 4.

Блок 3. r₁ := a₁₃N; r₂ := a₂₃N; r₃ := a₃₃N;

Блок 4. S := a₁₂ * r₁ + a₂₂ * r₂ + a₃₃ * r₃.

Включив указанные операции в блоки 3 и 4 схемы, соответственно получим подробную схему алгоритма всей задачи: