Рассмотрим несколько классов задач, решение которых требует составления разветвляющихся алгоритмов.
I. Существуют задачи, связанные с вычислением функций, заданных несколькими арифметическими выражениями (формулами). Это очень распространенные задачи, особенно в инженерных и экономических расчетах. Приведем пример такой задачи.
Задача 1.1. Вычислить значение Y по одной из формул:
| Y = { | X + a | если X < 10 | (1) |
| X — b1 | если 10 <= X <= 20 | (2) | |
| c + b2 | если 20 < X < 30 | (3) | |
| c — b3 | если 30 <= X | (4) |
где X = 3√a + b1.
Здесь b1, b2, b3 будем рассматривать как элементы массива В(1:3).
Условие задачи означает, что У зависит от X, а X может принимать любое значение из интервала (-∞, +∞). Этот интервал разбит на четыре области и в пределах каждой области У вычисляется по одной из формул. Значение х = 10 является границей для первой и второй областей; х = 20 — для второй и третьей, а х = 30 — для третьей и четвертой областей.
Решение.
1. Исходные данные: с, а, B(1:3). Результаты: X, У.
2. Метод решения задачи (в общем виде):
— ввод с, а, B(1:3);
— вычисление X;
— вычисление Y;
— вывод X, У.
3. Укрупненная схема алгоритма (фрагмент схемы) показана ниже.

Рассмотрим подробно блок 2 этой схемы.
Метод решения задачи: он должен обеспечить выявление области, которой принадлежит значение X, для чего достаточно проверить заданные условия по порядку, например, сверху вниз:
| Проверяем Х < 10, | если условие истинно (Да), вычисляем У = Х + а; если условие ложно (Нет), проверяем: |
| 10 <= X <= 20, | если Да, вычисляем У = Х — b1; если Нет, проверяем: |
| 20 < Х < 30, | если Да, вычисляем Y = c + b2; если Нет, вычисляем У = с — b3 |
Процесс решения задачи распадается на этапы (операции):
— «проверка истинности условия»,
— «вычисление по формуле».
Согласно Основным принципам алгоритмизации, заменяем каждую такую операцию соответствующим блоком — ромбом, прямоугольником и соединяем согласно порядку их выполнения линиями. В итоге получаем схему блока 2. Объединив ее с блоками 1 и 3, получим схему алгоритма всей задачи.
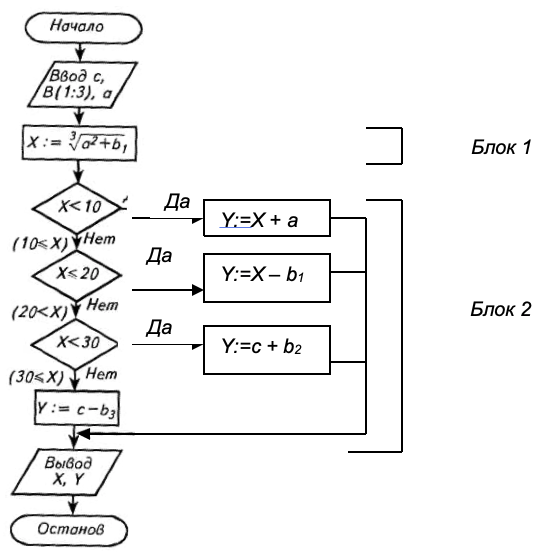
Изображая в схеме логический блок, следует выяснить и указать в явном виде, какому условию отвечает проверяемая переменная (в нашем случае — X) на выходе Нет этого блока. Полученную информацию следует использовать при реализации последующих условий. Так, для проверки условия (2) нашей задачи (10 <= X <= 20) достаточно проверить отношение Х <= 20, поскольку на входе второго логического блока отношение 10 <= Х всегда истинно. Аналогично для проверки условия (3) достаточно проверить одно отношение: Х < 30; информация на выходе Нет третьего логического блока (условие 30 <= Х - истинно) позволяет исключить отдельный блок для проверки условия (4).
II. Еще один распространенный вид задач — логические (так их иногда называют). К ним относятся задачи определения минимума, максимума некоторого числа величин, задачи упорядочивания, сортировки данных, многие задачи обработки массивов. В таких задачах доля арифметических операций обычно мала. Это достаточно сложные задачи, однако в простейших случаях при небольшом числе данных они приводят к построению несложных алгоритмов разветвляющейся структуры. Рассмотрим примеры подобных задач.
Задача 2.1. Определить Y = max { X,Z }.
Решение.
1. Исходные данные: X, Z. Результат: Y.
2. Метод решения задачи очевиден и предполагает выполнение трех основных операций. Применяя основные принципы алгоритмизации, получим схему алгоритма. Фрагмент ее приведен на рисунке ниже.

Задача 2.2. Определить значение наибольшего элемента главной диагонали матрицы А(1:3, 1:3).
Решение.
1. Исходные данные:
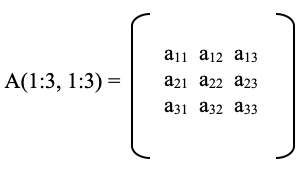
2. Результат: Y, т. е. Y = max {a11, a22, a33}.
Рассмотрим два варианта решения задачи.
Первый вариант.
Метод решения задачи:
проверяем a11 > a22
если Да, проверяем а11 > а33
Если Да — Y = a11
Если Нет — Y = a33
если Нет, проверяем а22 > а33
Если Да — Y = a22
Если Нет — Y = a33
Изображая каждую операцию этого процесса соответствующим блоком, согласно основным принципам алгоритмизации, получим схему алгоритма, фрагмент которой приведен на рисунке ниже.
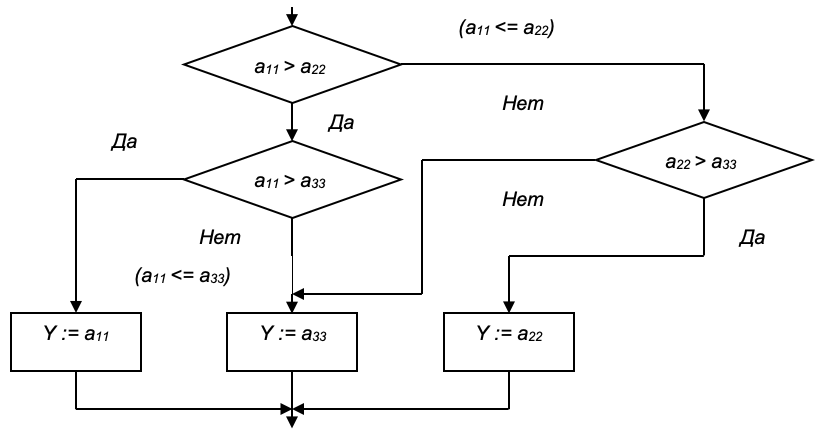
Второй вариант.
Метод решения задачи:
— ввод А(1:3, 1:3);
— определение Z = max{a11, a22};
— определение Y = max{Z, a33};
— вывод Y.
Укрупненная схема алгоритма, отражающая этот процесс (точнее, ее фрагмент), приведена на рисунке ниже.

Теперь составим схемы алгоритмов каждого из блоков 1 и 2 в отдельности. Они аналогичны схеме алгоритма задачи 2.1. Объединяя эти схемы, получим подробную схему алгоритма всей задачи:
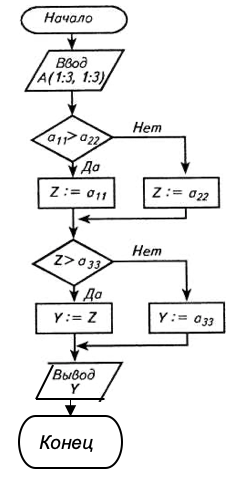
Вывод. Сравнение двух схем одной и той же задачи показывает, что в данном случае подход, основанный на разбиении задачи на независимые подзадачи и составлении укрупненной схемы, более эффективен. Этот вывод, как показывает опыт, справедлив и в общем случае.
III. Часто встречаются задачи, в которых используются не только простые условия, но и составные, (использование условий с операциями и, или, не).
Например, контролер ОТК завода решает задачу — отобрать из числа изготовленных болты длиной Z, допустим 18 мм, и диаметром d не менее 7 мм и не более 8 мм.
Другой пример: школьник выяснил, что сможет попасть в кино при условии, если в кассе есть билеты по цене 40 или 50 руб.
В первом примере мы имеем дело с тремя отношениями, связанными между собой союзом «и» и частицей «не», во втором — с двумя отношениями, связанными союзом «или».
Условия наших примеров в алгоритме могут выглядеть в виде составных условий таким образом:
первое — (l = 18) и (не (d <= 7)) и (не (d > 8)) или, что то же: (l = 18 и d >= 7 и d <= 8);
второе — С = 40 или С = 50.
Реализация логических выражений (составных условий). Возможны два подхода к составлению алгоритмов задач, содержащих составные условия.
1. Составное условие рассматривается как «единое и неделимое» и в схеме изображается одним логическим блоком. Такой подход допустим, если в языке программирования, на который мы ориентируемся, составные условия разрешены.
2. Для каждого составного условия изображается схема алгоритма, реализующая ее. В такой схеме каждое отношение составного условия изображается отдельным логическим блоком.
Подобная схема имеет два выхода (Да и Нет) и обеспечивает «передачу управления» (так принято говорить) на один выход, если составное условие выполняется, и на другой — если оно не выполняется.
Этот подход неизбежен, если используемый язык программирования не допускает применения составных условий.
Задача 3.1. Вычислить значение Y по одной из формул:
| Y = { | X + Z | если Х < 10 и Z > 5 |
| X * Z | в остальных случаях |
Решение.
Составим схему алгоритма задачи, используя второй подход. Метод решения задачи вытекает из определения составного условия «А и В»:
проверяем Х < 10
если Да, проверяем Z > 5
если Да — Y = X + Z
если Нет — Y = X * Z
если Нет — Y = X * Z
Руководствуясь основными принципами алгоритмизации, составляем схему алгоритма задачи:
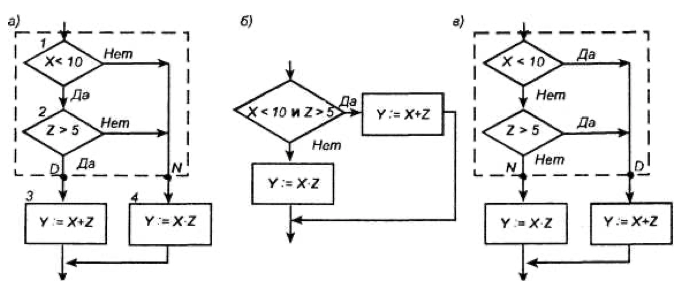
Здесь блоки 1 и 2 образуют схему, реализующую составное условие «А и В». Точки D и N — выходы Да и Нет соответственно схемы, реализующей указанное условие. Отметим, что при использовании первого подхода алгоритм решения задачи описывается простейшей схемой.