Разветвляющимся называется такой алгоритм, в котором выбирается один из нескольких возможных путей (вариантов) вычислительного процесса. Каждый подобный путь называется ветвью алгоритма. Примером такого алгоритма является алгоритм решения задачи расчета заработной платы.
Признаком разветвляющегося алгоритма является наличие операций проверки условия. Обычно различают два вида условий — простые и составные.
Простым условием (отношением) называется выражение, составленное из двух арифметических выражений или двух текстовых величин, связанных одним из знаков: <, >, = и т.д. Примеры отношений:
X + Y < 7
Y > ln Z
R <= X2 + √ D
2 ≠ 3
«МАМА» ≠ «ПАПА»
В = «ДА» (В — текстовая переменная)
Составные условия можно образовать путем составных (сложных) логических выражений, с помощью логических операций И, ИЛИ, НЕ.
Примеры составных логических выражений:
X < 7 И X > 2
X = 2 ИЛИ X = 3 ИЛИ X = 2145
Y > 0 ИЛИ (Y < 0 И X < 0)
В схеме алгоритма операцию проверки условия выполняет логический блок. Он изображается ромбом, внутри которого указывается проверяемое условие (отношение), и имеет два выхода: Да и Нет.
Если условие (отношение) истинно (выполняется), то выходим из блока по выходу Да; если ложно (не выполняется) — по выходу Нет.
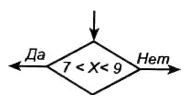
Условие (отношение), содержащееся в логическом блоке, может быть заменено на противоположное:
Х < 10 -> Х > 10
K = 15 -> K ≠ 15
При этом выходы Да и Нет меняются местами.
Логический блок может содержать лишь одно условие. В соответствии с этим блок, представленный на рисунке выше, записан неверно, так как двойное неравенство 7 < Х < 9 содержит фактически два простых условия: 7 < Х и Х < 9.
Типовая схема разветвляющегося алгоритма. Несмотря на большое разнообразие разветвляющихся алгоритмов, желательно все же добиваться некоторого однообразия их структуры, для чего следует приводить их к виду схемы, представленной на рисунке ниже. Хотя это и не всегда возможно, но к этому нужно стремиться.
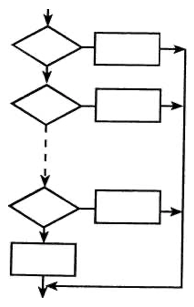
Подобный подход позволяет строить простые и однообразные по структуре программы, а значит, и легко понимаемые.