Пусть задано бинарное отношение f ⊆ A×B.
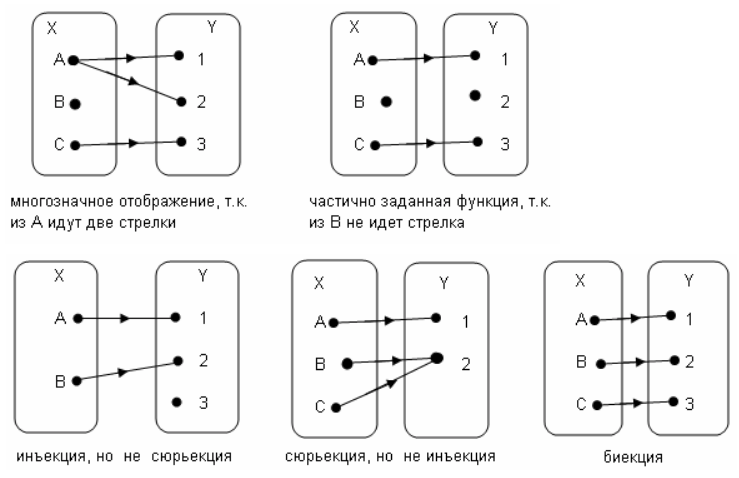
Определение. Отношение f ⊆ A×B называется многозначным отображением, если f задает правило, по которому некоторым (не обязательно всем) элементам x∈A ставится в соответствие один или несколько элементов y ∈ B.
Определение. Отношение f ⊆ A×B называется функцией (однозначным отображением), если f задает правило, по которому каждому элементу x ∈ A ставится в соответствие только один элемент y ∈ B.
Замечание. Если отношение f ⊆ A×B задает правило, по которому некоторым (не обязательно всем) элементам x ∈ A ставится в соответствие только один элемент y ∈ B, то оно называется частичной функцией.
Обозначается функция следующим образом: f:А→В. Часто на практике используется и префиксная форма записи − y = f(x), в этом случае x называют аргументом, а y — значением функции f.
Замечание. Если в определении функции f множество A = A1 × A2 × … × An, то функция f называется функцией n аргументов.
Определение. Функция f:A→B называется:
— иньективной (отображением «в»), если разным x1 и x2 (x1 ≠ x2) из A, соответствуют разные у1 и y2 (y1 ≠ y2) из B;
— сюрьективной (отображением «на»), если для любого элемента b ∈ B найдется элемент a ∈ A такой, что b = f(a);
— биективной или взаимнооднозначной, если она инъективная и сюръективная.
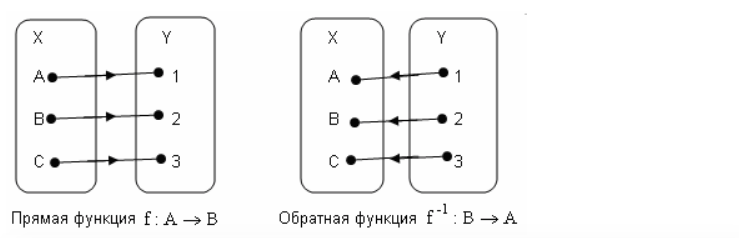
Теорема. Если f:А→В — биекция, то отношение f-1:В→А (обратная функция) является биекцией.
Теорема. Если f:А→В — инъекция, но не сюръекция, то отношение f-1:В→А (обратная функция) является частично определенной функцией.
Теорема. Пусть A и B конечные множества. Биекция f:А→В существует тогда и только тогда, когда множества A и B имеют одинаковое число элементов.
Определение. Пусть f:A→B функция.
— Образом множества A1 ⊆ A называется множество f(A1) = {b|b ∈ B и существует x ∈ A1, что b = f(x)}.
— Пробразом множества B1 ⊆ B называется множество f-1(B1) = {a|a ∈ A и существует y ∈ B1, что y = f(a)}.
— Областью определения (частичной) функции f называется множество элементов из A, для которых существуют образы в B;
— Областью значений функции называется множество элементов из B, для которых существуют прообразы в A.
Пример. Пусть заданы множества A = {1, 2, 3, 4, 5}, В = {a, b, c, d} и функция f:A→B, которая изображена на рисунке.
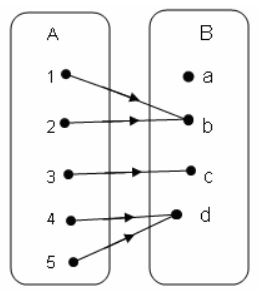
f({1, 2}) = {b}
f({4}) = {d}
f({2, 5}) = {b, d}
f({2, 3, 5}) = {b, c, d}
f-1({b}) = {1, 2}
f-1({b, d}) = {1,2,4,5}
f-1({a}) = ∅.
Область определения f = {1, 2, 3, 4, 5} = A, область значений f = {b, c, d} ⊂ B.