Пусть R — бинарное отношение на множестве А, т.е. R⊂А².

Отношение R называется отношением строгого порядка, если оно антирефлексивно, антисимметрично и транзитивно. Обычно обозначается < или >.

Отношение R называется отношением частичного порядка (нестрогого порядка), если оно рефлексивно, антисимметрично и транзитивно. Обычно обозначается ≤ или ≥.

Множество A с заданным частичным порядком ≤ называется частично упорядоченным множеством (ч.у.м.) и обозначается (A, ≤). Отметим, что в частично упорядоченном множестве не все элементы могут быть связаны отношением ≤ (сравнимы между собой). Если все элементы ч.у.м. (A, ≤) сравнимы между собой, то множество называется линейно упорядоченным, а порядок ≤ в этом случае называется линейным.

Очевидно, что отношение строгого порядка не является отношением частичного порядка.

Пример. Линейным порядком является обычное отношение ≤ на множестве натуральных чисел N, т.к. для любых чисел x, y выполняется или x ≤ y или y ≤ x.

Пример. Отношение, изображенное на рисунке ниже, является частичным порядком.

Пример. Отношение включения ⊆ на булеане 2^U образует частичный порядок. Очевидно, что если множества А и В не пересекаются, то они не сравнимы между собой.

Пример. Определим на множестве А² отношение ≤ условием: (a, b) ≤ (а₁, b₁) ⇔ a ≤ a₁ и b ≤ b₁. Отношение ≤ есть отношение частичного порядка. Оно называется отношением Парето. Так вектора (0, 3) и (2, 3) сравнимы между собой: (0, 3) ≤ (2, 3), т.к. 0 ≤ 2 и 3 ≤ 3. Очевидно, что вектора (2, 1) и (0, 3) не сравнимы между собой.

Элемент а ∈ А частично упорядоченного множества U = (А, ≤) называется максимальным (минимальным), если для всех x ∈ А из а ≤ х (х ≤ а) следует х = а. Элемент а ∈ А называется наибольшим (наименьшим), если х ≤ а (а ≤ x) для всех x ∈ А. Наибольший (наименьший) элемент ч.у.м. U (если он существует) обозначается через maxU (minU). Наибольший элемент часто называют единицей, а наименьший − нулем множества U.

Пример. Ч.у.м. ({A, B, C}, ≤), изображенное на рисунке ниже, имеет наибольший элемент B, минимальные элементы A, C, но не имеет наименьшего элемента.

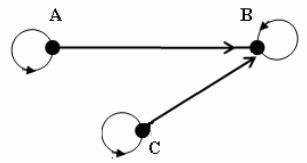
Теорема. Во всяком конечном непустом частично упорядоченном множестве существует минимальный элемент.

Теорема. Всякий частичный порядок на конечном множестве может быть дополнен до линейного.

Линейный порядок ≤ на множестве А называется полным, если каждое непустое подмножество множества А имеет наименьший элемент. Пара (А, ≤), в которой отношение ≤ является полным порядком на множестве А, называется вполне упорядоченным множеством (сокращенно в.у.м.).

Рассмотрим непустое множество символов Х = {x, y, z, …}, называемое алфавитам. Конечные, наборы написанных друг за другом символов из Х называются словами (например, x, у, ху, ух, zxx, xyyz и т. д.). Элемент x_i слова х₁, х₂, … x_n называется его i-й координатой. Число n называется длиной слова х₁, х₂, … x_n. Множество слов алфавита Х обозначим через W(X). При этом будем считать, что W(X) содержит слово ∧, не имеющее символов и называемое пустым словом. Длина пустого слова ∧ по определению равна нулю.

Пусть ≤ отношение порядка на множестве X. Определим на множестве W(X) отношение лексикографического порядка L по следующему правилу: х₁, х₂, … x_mLy₁, y₂, … y_n если выполняется одно из двух условий:

1. m ≤ n и х_i = у_i для всех 1 ≤ i ≤ n;

2. существует i ≤ m такое, что х_i < у_i, и для всех j < i выполняется х_j = у_j.

Утверждение. Если (X, ≤) — линейно упорядоченное множество (л.у.м.), то (W(X), L) — л.у.м.

Пример. Рассмотрим множество букв русского алфавита, которое обозначим через X. Определим на X полный порядок ≤ в соответствии с обычным упорядочением букв по алфавиту. Отношение L на множестве слов W(X) определяет упорядочение слов, по которому составляются словари русского языка.

Рассмотрим частично упорядоченное множество (А, ≤). Говорят, что элемент у покрывает элемент x, если x ≤ у и не существует такого элемента z, что х ≤ z ≤ у. Если множество А конечно, то частично упорядоченное множество (А, ≤) можно представить в виде схемы, в которой каждый элемент изображается точкой на плоскости, и если у докрывает х то точки х и у соединяют отрезком, причем точку, соответствующую x, располагают ниже у. Такие схемы называются диаграммами Хассе.

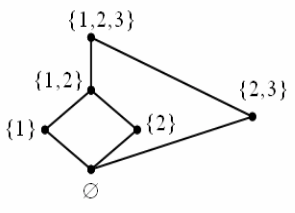
Пример. Рассмотрим частично упорядоченное множество (А, ⊆), где А = {∅, {1}, {2}, {1, 2}, {2, 3}, {1, 2, 3}}. На рисунке ниже изображена диаграмма Хассе, соответствующая (А, ⊆). Элемент ∅ ∈ А является наименьшим (minU = ∅), а {1, 2, 3} ∈ А наибольшим (minU = {1, 2, 3}).

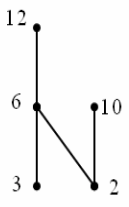
Пример. Пусть А = {2, 3, 6, 10, 12}. Рассмотрим отношение частичного порядка ≤ на множестве А, задаваемое по правилу: х ≤ у ⇔ у делится на х. Диаграмма Хассе для частично упорядоченного множества (А, ≤) изображена на рисунке ниже. Элементы 2 ∈ А и 3 ∈ А являются минимальными, а 10 ∈ А и 12 ∈ А максимальными. Наибольшего и наименьшего здесь нет.

Пример. На рисунке ниже изображена диаграмма Хассе линейно упорядоченного множества ({1, 2, 3, 4}, ≤) с обычным отношением порядка на множестве натуральных чисел, не превосходящих четырех.

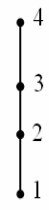
Заметим, что диаграммы Хассе двух отношений могут совпадать. Это означает, что эти частично упорядоченные множества имеют одинаковую структуру. Формально такая общность структуры определяется понятием изоморфизма.