Рассмотрим конечное множество А = {a₁, a₂, … a_n}, и бинарное отношение P на A: P⊂A². Определим матрицу [P] = (p_ij) порядка n бинарного отношения Р по следующему правилу:

Pij = {	1, если (ai, aj) ∈ P
	0, если (ai, aj) ∉ P

Полученная матрица содержит полную информацию о связях между элементами и позволяет представлять эту информацию на компьютере. Заметим, что любая матрица, состоящая из нулей и единиц, является матрицей некоторого бинарного отношения.

Пример 1. Матрица бинарного отношения P⊂А², где А = {1, 2, 3}, заданного на рисунке:

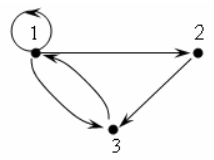
имеет вид:

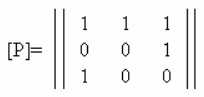
Отметим основные свойства матриц бинарных отношений заданных на множестве A.

1. Если P, Q⊂A×В, [Р] = (р_ij), [Q] = (q_ij), то [Р∩Q] = (p_ij · g_ij) и [Р∪Q] = (р_ij + q_ij), где сложение осуществляется по правилам алгебры логики (дизъюнкция) 0 + 0 = 0, 1 + 1 = 1 + 0 = 0 + 1 = 1, а умножение — обычным образом. Итак, [Р∪Q] = [Р]+[Q], а матрица [Р∩Q] получается перемножением соответствующих элементов из [Р] и [Q]:[P∪Q] = [P]·[Q].

Пример 2. Пусть $\mathrm{[P]\; =}\left(\begin{array}{c}011\\ 110\\ 010\end{array}\right)$ , $\mathrm{[Q]\; =}\left(\begin{array}{c}001\\ 010\\ 110\end{array}\right)$ матрицы отношений Р и Q. Тогда $\mathrm{[Р\cup Q]\; =}\left(\begin{array}{c}011\\ 110\\ 110\end{array}\right)$, $\mathrm{[Р\cap Q]\; =}\left(\begin{array}{c}001\\ 010\\ 010\end{array}\right)$.

2. Если Р⊂A×В, Q⊂В×С, то [P°Q] = [Р]×[Q], где умножение матриц [Р] и [Q] производится по обычному правилу умножения матриц («строка на столбец»), но произведение и сумма (дизъюнкция) элементов из [Р] и [Q] — по определенным в п. 1 правилам.

Пример 3. Пусть [Р], [Q] − матрицы отношений Р и Q из примера 1. Тогда $$\mathrm{[P°Q]\; =}\left(\begin{array}{ccc}\mathrm{0+0+0}& \mathrm{0+1+1}& \mathrm{0+0+0}\\ \mathrm{0+0+0}& \mathrm{0+1+0}& \mathrm{1+0+0}\\ \mathrm{0+0+0}& \mathrm{0+1+0}& \mathrm{1+0+0}\end{array}\right)\mathrm{=}\left(\begin{array}{c}010\\ 011\\ 011\end{array}\right)$$

3. Матрица обратного отношения Р^-1 равна транспонированной матрице отношения Р: [Р^-1] = [Р]^t.

Пример 4. Пусть $\mathrm{[}P\mathrm{]}\mathrm{=}\left(\begin{array}{c}011\\ 110\\ 010\end{array}\right)$ , $\mathrm{[}{P}^{-1}\mathrm{]}\mathrm{=}\left(\begin{array}{c}010\\ 111\\ 100\end{array}\right)$ .

4. Если Р⊂Q, [Р] = (р_ij), [Q] = (q_ij), то [Р] ≤ [Q], что означает p_ij ≤ q_ij ∀i,j. Верно и обратное, если [Р] ≤ [Q] , то Р⊂Q.

5. Матрица тождественного отношения [I_A] — единична.

Теорема. Пусть R — бинарное отношение на множестве А (R⊂А²).

1. R рефлексивно ⇔ [I_A] ≤ [R], т.е. на главной диагонали матрицы [R] стоят только единицы;

2. R антирефлексивно ⇔ на главной диагонали матрицы [R] стоят только нули.

3. R симметрично ⇔ [R] — симметричная матрица, т.е. [R] = [R]^t;

4. R антисимметрично ⇔ [R^-1∩R] ≤ [I]_A, т.е. вне главной диагонали все элементы равны нулю;

5. R транзитивно ⇔ [R°R] ≤ [R].