Определение. n-местным (n-арным) отношением R на множествах A₁,A₂,…,A_n называется подмножество декартового произведения A₁×A₂×…×A_n, т.е. R ⊆ A₁×A₂×…×A_n.

При n = 1 отношение R является подмножеством множества A и называется унарным отношением или свойством.

При n = 2 отношение R называется бинарным отношением (т.е. R ⊆ A×B — бинарное отношением).

Из определения отношения R следует, что R является множеством и поэтому, во-первых, может быть задано как множество, а во-вторых, все теоретико-множественные операции и рассуждения распространяются и на отношения.

Для бинарных отношений часто используется инфиксная форма записи: aRb = {(a,b)|R ⊆ A×В}. Если A = B, то говорят, что R есть бинарное отношение на множестве А.

Примеры.

1. Если А = {2,3,4,5,6,7,8}, то бинарное отношение Р = {(x,у)|x∈А, у∈A, x делит у и x < 4} можно записать в виде P = {(2,2), (2,4), (2,6), (2,8), (3,3), (3,6)}.

2. Отношение быть отцом на множестве группы людей. Здесь запись aRb означает, что a является отцом b.

3. Отношение параллельности на множестве всех прямых на плоскости. Здесь запись aRb означает, что прямая a параллельна прямой b.

4. Числа x, y связаны отношением R, если они являются корнями уравнения sinx = 0.5, т.е. R = {x| sinx = 0.5 и x действительное число}.

5. Многоместные отношения используются, например, в теории баз данных. Само название «реляционная» база данных происходит от слова relation (отношение). В качестве примера рассмотрим базу данных телефонного справочника, которая состоит из трех полей (множеств): A₁ = {фамилия, имя, отчество абонента}, A₂ = {номера телефонов}, A₃ = {адрес абонента}. Декартовое произведение A₁×A₂×A₃ лишь обозначает структуру базы данных, показывая, что в записи на первом поле будет выведено фамилия, имя, отчество абонента, на втором поле номер телефона абонента, а на третьем адрес абонента. Отношение R задает базу данных, т.к. из всех возможностей однозначно определяет, какому абоненту соответствует тот или иной номер телефона и адрес.

Замечание. По сути, все связи между различными объектами являются отношениями.

Определение. Пусть R⊆A×B бинарное отношение. Множество X = {x|x∈A и (x,y)∈R для некоторого y∈B} называется областью определения отношения R. Множество Y = {y| y∈B и (x,y)∈R для некоторого x∈A} называется областью значений отношения R.

Определения. Пусть R бинарное отношение на множестве A.

Отношение R^-1 = {(x,y)|(y,x)∈R} − называется обратным отношением.

Отношение I_A = {(x,x)|x∈A} − называется тождественным отношением.

Отношение U_A = {(x,y)|x∈A и y∈A} = A×A − называется универсальным отношением.

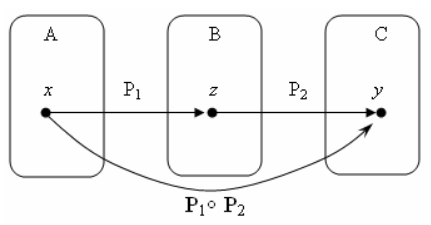
Определение. Пусть P₁⊆A×B, P₂⊆B×C − два бинарных отношения.

Композицией отношений P₁ и P₂ (обозначается P₁°P₂) называется множество P₁°P₂ = {(x,у)|х∈A, у∈C, и найдется элемент z∈B такой, что (x,z)∈P₁ и (z,y)∈P₂}.

Отметим, что частным случаем композиции отношений является хорошо известное понятие сложной функции, например, y = sin(ln(x)). Схема действия композиции двух отношений может быть проиллюстрирована следующим образом: