Введение понятий «множество» и «элемент множества» еще недостаточно для эффективной работы с множествами, еще нужно определить способы конструирования новых множеств из уже имеющихся, т.е. ввести операции над множествами.

1. Объединением двух множеств A и B (обозначается A∪B) называется множество элементы которого принадлежат либо А, либо В, либо обоим множествам сразу (другими словами, хотя бы одному множеству А или В).

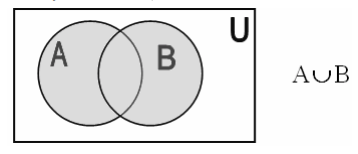
2. Пересечением двух множеств A и B (обозначается A∩B) называется множество элементы которого принадлежат А и В одновременно.

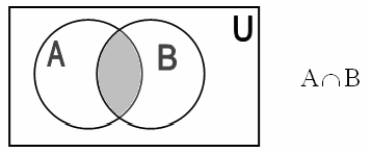
Два множества называются непересекающимися, если они не имеют общих элементов, т.е. A∩B = ∅.

3. Разностью двух множеств A и B (обозначается A\B) называется множество элементы которого принадлежат А, но не принадлежат В (читается А минус В).

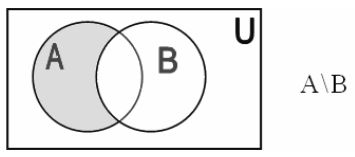
Очевидно, что если множества A и B не равны, то A\B ≠ B\A.

4. Симметричной разностью двух множеств A и B (обозначается A∆B ИЛИ A⊕B) называется множество элементы которого принадлежат А, или B, но не обоим сразу (часто читается «А плюс В»).

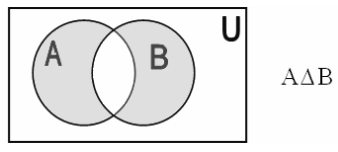
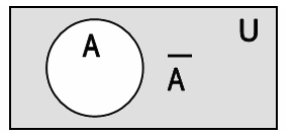
5. Дополнением множества A (обозначается ¬A) называется множество, элементы которого не принадлежат А.

Утверждение.

1. A∆B = (A\B)∪(B\A).

2. A∆B = (A∪B)\(B∩A).

3. ¬A = U\A.

4. Если множества A и B не пересекаются, то A\B = A.