Пусть задан универсум U. Тогда для любых множеств A, B, C ⊆ U выполняются следующие свойства:

1. идемпотентность: A∩A = A, A∪A = A;

2. коммутативность: А∪В = В∪А, А∩В = В∩А;

3. ассоциативность: А∩(В∩С) = (А∩В)∩С, А∪(В∪С) = (А∪В)∪С;

4. дистрибутивность: А∩(В∪С) = (А∩В)∪(А∩С), А∪(В∩С) = (А∪В)∩(А∪С);

5. поглощение: (A∪B)∩A = A, (A∩B)∪A = A;

6. свойства нуля (∅): A∩∅ = ∅, A∪∅ = A;

7. свойства единицы (U): A∩U = A, А∪U = U;

8. инволютивностъ: ¬(¬A) = A;

9. законы де Моргана: ¬(A∩B) = ¬A∪¬B , ¬(A∪B) = ¬A∩¬B ;

10. свойства дополнения: A∪¬A = U , A∩¬A = ∅.

В справедливости перечисленных свойств можно убедиться различными способами. Например так, нарисовать диаграммы Венна для левой и правой частей равенства, а затем визуально убедиться, что они совпадают. Другой способ, это провести формальное рассуждение для каждого равенства.

Докажем, например, равенство А∪(В∩С) = (А∪В)∩(А∪С).

1-й способ.

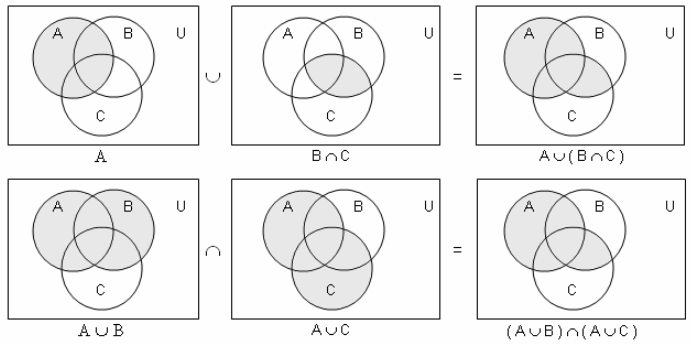
2-й способ.

Пусть х ∈ А∪(В∩С). Тогда из определения объединения множеств следует, что либо х ∈ А, либо х ∈ В∩С, либо обоим множествам одновременно. Если х ∈ А, то х ∈ А∪В и х ∈ А∪С, а, следовательно, по определению пересечения множеств х ∈ (А∪В)∩(А∪С). Если х ∈ В∩С, то х ∈ В и х ∈ С. Следовательно, х ∈ А∪В и х ∈ А∪С. Отсюда имеем, что х ∈ (А∪В)∩(А∪С). Таким образом, доказано что, А∪(В∩С) ⊆ (А∪В)∩(А∪С). Аналогично доказывается и обратное, т.е., что (А∪В)∩(А∪С) ⊆ А∪(В∩С). Следовательно, по определению равенства множеств получаем, А∪(В∩С) = (А∪В)∩(А∪С).