Пусть R⊂А² − бинарное отношение на множестве A. Тогда отношение R называется:

— рефлексивным, если для любого a∈A следует, что (a,a)∈R;

— антирефлексивным, если для любого a∈A следует, что (a,a)∉R;

— симметричным, если для всех a,b∈A связанных отношением R (т.е. (a,b)∈R), следует, что (b,a)∈R;

— антисимметричным, если для любых a,b∈A таких, что (a,b)∈R и (b,a)∈R, следует, что a=b;

— транзитивным, если для любых a,b,c∈A таких, что (a,b)∈R и (b,c)∈R, следует, что (a,c)∈R;

Теорема. Пусть R⊂А² − бинарное отношение на A. Тогда:

1. R рефлексивно ⇔ I_A⊆R, где I_A = {(x, x)|x∈A} − тождественное отношение;

2. R антирефлексивно ⇔ I_A∩R = ∅.

3. R симметрично ⇔ R^-1 = R;

4. R антисимметрично ⇔ R^-1∩R⊂I_A;

5. R транзитивно ⇔ R°R⊂R.

В более общей ситуации мы можем интерпретировать рассмотренные выше характеристики отношения путем построения диаграммы:

а) отношение рефлексивно тогда и только тогда, когда для каждого узла (точки) на диаграмме существует стрелка, которая начинается и заканчивается на этом узле (петля);

б) отношение антирефлексивно тогда и только тогда, когда для каждого узла на диаграмме не существует петли;

в) отношение симметрично тогда и только тогда, когда для каждой стрелки, соединяющей два узла, существует также стрелка, соединяющая эти узлы в обратном направлении;

г) отношение антисимметрично тогда и только тогда, когда не существует двух различных узлов, связанных парой стрелок, т.е. если есть стрелка (x, y), то нет стрелки (у, x).

д) отношение транзитивно тогда и только тогда, когда для каждой пары узлов x и у, связанных последовательностью стрелок (путем) идущих от x к a₁, от а₁ к a₂, …, от am_-1 к a_m, от а_m к у, существует также стрелка идущая напрямую от x к у;

Пример. Рассмотрим отношение R, изображенное на рисунке:.

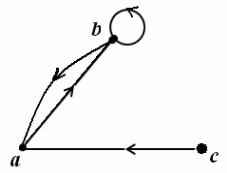
R не является рефлексивным (нет петель на узлах a и c);

R не является антирефлексивным, т.к. есть петля на узле b,

R не является симметричным, т.к. есть стрелка (c, a), но нет стрелки (a, c);

R не является антисимметричным, т.к. есть стрелки (a, b) и (b, a);

R не является транзитивным, т.к., например, есть стрелки (a, b) и (b, a), но нет стрелки (a, a).