Ниже описываются четыре различных базовых представления графов в ЭВМ. Выбор наилучшего представления определяется требованиями конкретной задачи. Более того, при решении задач используются, как правило, некоторые комбинации или модификации указанных представлений. Но все они, так или иначе, основаны на тех базовых идеях, которые описаны в этом разделе.
А) Матрица смежности.
Пусть G = (V, E) граф (орграф) с p-вершинами и q ребрами, т.е. V = {v1, v2, …, vp}, E = {e1, e2, …, eq}.
Матрицей смежности графа (орграфа) G называется квадратная матрица A(G) порядка p элементы которой равны:
| aij = { | 1, если (vi, vj) ∈ E |
| 0, если (vi, vj) ∉ E |
Замечание 1. Матрица смежности A:array[l..p, l..p] of 0..1, отражает смежность вершин. Преимущество такого представления является «прямой доступ» к ребрам графа, т.е. за один шаг получаем ответ на вопрос «существует ли в графе ребро (a, b)». Недостаток же заключается в том, что независимо от числа ребер объем занимаемой памяти равен p2 для орграфа и p2/2 для графа.
Пример. Граф G и орграф D изображены на рисунке ниже. Найдем их матрицы смежности.


Замечание 2. Матрица смежности для неориентированного графа является симметричной.
Замечание 3. Матрицу смежности можно ввести для мультиграфов: элемент aij матрицы A равен числу ребер (дуг) идущих из вершины vi к вершине vj.
Б) Матрица инцидентности.
Пусть G = (V, E) граф (орграф) с p-вершинами и q ребрами, т.е. V = {v1, v2, …, vp}, E = {e1, e2, …, eq}.
Матрицей инцидентности B(G) орграфа G называется матрица порядка p×q, элементы которой вычисляются следующим образом:
| bij = { | 1, если vi является концом дуги ej |
| -1, если vi является началом дуги ej | |
| 0, если vi не инцидентна дуге ej |
Матрицей инцидентности B(G) графа G называется матрица порядка p×q, элементы которой вычисляются следующим образом:
| bij = { | 1, если vi инцидентна ребру ej |
| 0, если vi не инцидентна ребру ej |
Замечание 4. В каждом столбце матрицы инцидентности только два элемента не равны нулю (они равны ±1).
Замечание 5. Матрицу инцидентности можно ввести для псевдографов: например, элемент aij матрицы A равен +1, если вершина vi является началом и концом дуги ej , все остальные элементы в этом столбце равны нулю.
Замечание 6. Недостаток этого способа заключается в том, что объем занимаемой памяти равен p·q, причем большинство из ячеек памяти равны 0. Кроме того, неудобен доступ на элементарные вопросы, типа «существует ли в графе ребро (a, b)» или «К каким вершинам ведут ребра из вершины a?». В этом случаи может потребоваться перебор всех ребер графа G.
Пример. Граф G и орграф D изображены на предыдущем рисунке. Найдем их матрицы инцидентности.

В) Списки смежности.
Представление графа с помощью списочной структуры, отражающей смежность вершин и состоящей из массива указателей A:array [l..p] of ↑ N на списки смежных вершин называется списком смежности. Элемент списка представлен структурой N:

Элементы списка смежности имеют структуру info.
Пример. Пусть граф G и орграф D изображены на рисунке выше. Найдем их списки смежности.
Способ 1.
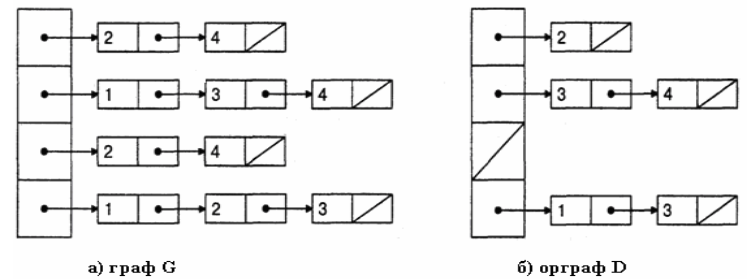
Способ 2.

Г) Список ребер.
Для описания каждого ребра требуется по две ячейки памяти (по одной на каждую из двух концевых вершин ребра). Объем занимаемой памяти составляет 2·q. Неудобством является нахождение списка смежных вершин для отдельно взятой вершины. Пример задания списка ребер для графа, изображенного так же на рисунке выше.

Очевидно, что список ребер можно организовать заданием двух массивов, в которых индекс будет однозначно указывать на ребро.