Очевидно, что каждый неориентированный граф можно сделать ориентированным, заменив каждое ребро парой дуг идущих в противоположных направлениях (см. рисунок ниже). В связи с этим, можно рассматривать «смешанные» графы, которые могут содержать и ребра и дуги. Очевидно, что графы и орграфы являются частными случаями «смешанных» графов. В том параграфе под словом «граф» понимается «смешанный» граф, а под словом «ребро», понимается либо ребро, которое обозначаться будет [u, v], либо дуга, которая обозначаться будет (u, v).

Напомним, что граф состоит из пары множеств, для которых теоретико-множественные операции рассмотрены в главе Маршруты, пути, циклы.

Граф G₁ = (V₁, E₁) называется подграфом графа G = (V, E), если V₁⊆V и E₁⊆E. Подграф G₁ называется собственным подграфом графа G, если G₁ не совпадает с G.

Определения. Пусть даны два графа G₁ = (V₁, E₁) и G₂ = (V₂, E₂).

1. Пересечением двух графов G₁ и G₂ называется граф G = (V, E), где V = V₁∩V₂, E = E₁∩E₂. Обозначение: G = G₁∩G₂.

2. Объединением двух графов G₁ и G₂ называется граф G = (V, E), где V = V₁∪V₂, E = E₁∪E₂. Обозначение: G = G₁∪G₂.

3. Симметрической разностью (или суммой по модулю 2) двух графов G₁ и G₂ называется граф G = (V, E), где V = V₁∪V₂, E = E₁⊕E₂ (E = E₁∆E₂). Обозначение: G = G₁⊕G₂.

4. Пусть задан граф G = (V, E) c |V| = n (т.е. с n вершинами) и без петель. На множестве вершин V построим полный граф K_n = (V, M). Дополнением графа без петель G(V, E) называется граф G’ = (V, M\E).

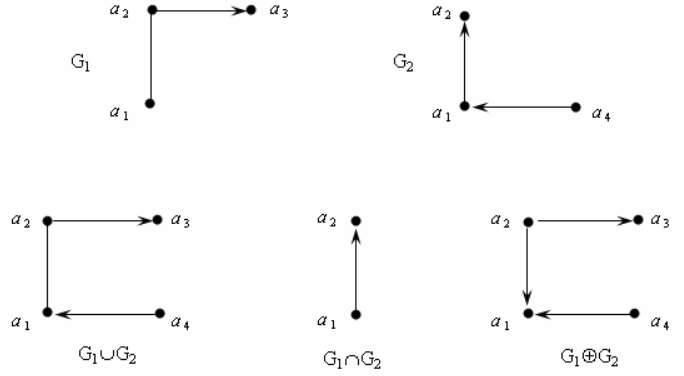
Пример. Пусть даны графы G₁ = (V₁, E₁) и G₂ = (V₂, E₂), где V₁ = {a₁, a₂, a₃}, E₁ = {[a₁, a₂], (a₂, a₃)}, V₂ = {a₁, a₂, a₄}, E₂ = {(a₁, a₂), (a₄, a₁)} (см. рисунок ниже).

1. Найдем G = G₁∪G₂ = (V, E), где V = {a₁, a₂, a₃}∪{a₁, a₂, a₄} = {a₁, a₂, a₃, a₄}, Е = {[a₁, a₂], (a₂, a₃)}∪{(a₁, a₂), (a₄, a₁)} = {[a₁, a₂], (a₂, a₃), (a₄, a₁)}.

2. Найдем G = G₁∩G₂ = (V, E), где V = {a₁, a₂, a₃}∩{a₁, a₂, a₄} = {a₁, a₂}, Е = {[a₁, a₂], (a₂, a₃)}∩{(a₁, a₂), (a₄, a₁)} = {(a₁, a₂)}.

3. Найдем G = G₁⊕G₂ = (V, E), где V = {a₁, a₂, a₃}∪{a₁, a₂, a₄} = {a₁, a₂, a₃, a₄}, Е = {[a₁, a₂], (a₂, a₃)}⊕{(a₁, a₂), (a₄, a₁)} = {(a₂, a₁), (a₂, a₃), (a₄, a₁)}.

Пример. Дополнением графа G, изображенного на рисунке ниже слева, является граф G’, изображенный на рисунке ниже справа.