Пусть G = (V, E) граф с p вершинами и q ребрами, т.е. V = {v1, v2, …, vp}, E = {e1, e2, …, eq}.
Маршрутом, соединяющим вершины vn0, vni в графе G, называется чередующаяся последовательность вершин и ребер, в которой любые два соседних элемента инцидентны: vno en1 vn1 en2 vn2 … eni vni. Вершины vno, vni называются начальной и конечной вершинами маршрута, остальные называются внутренними. Число ребер в маршруте называется длиной маршрута.
Замечание. Это определение подходит также для псевдо-, мульти- и орграфов. Для «обычного» графа часто указывают только последовательность вершин или только последовательность ребер, т.к. оставшиеся компоненты в этом случае восстанавливаются однозначно.
Если начальная и конечная вершины маршрута совпадают (vn0 = vni), то маршрут называется замкнутым, иначе − открытым.
Если все ребра в маршруте различны, то маршрут называется цепью. Если все вершины (а значит и ребра) в маршруте различны, то маршрут называется простой цепью. В цепи начальная и конечная вершины называются концами цепи. Говорят, что цепь с концами u и v соединяет вершины u и v. Цепь, соединяющая вершины u и v, обозначается <u, v>. Очевидно, что если есть цепь, соединяющая вершины u и v, то есть и простая цепь, соединяющая эти вершины. Замкнутая цепь называется циклом, а замкнутая простая цепь называется простым циклом. Граф без циклов называется ациклическим.
Замечание. Часто в записи замкнутого маршрута перечисляют только вершины входящие в маршрут, тем самым, подчеркивая, что в этом случае неважно какую вершину считать начальной.
Для орграфов цепь называется путем, а цикл — контуром. Отметим, что двигаться в орграфе можно только в направлении «стрелок».
Пример. Найти в графе G, диаграмма которого приведена на рисунке, маршрут, цепь, простую цепь.
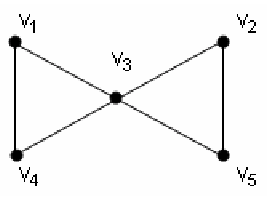
1. v1v3v1v4 — маршрут длины 3, но не цепь;
2. v1v3v5v2v3v4 — цепь длины 5, но не простая цепь;
3. v1v4v3v2v5 — простая цепь длины 4;
4. v1v3v5v2v3v4v1 — цикл длины 6, но не простой цикл;
5. v1v3v4 — простой цикл длины 3.
Определения.
1. Расстоянием между вершинами u и v называется длина кратчайшей цепи <u, v>. Расстояния между вершинами удобно изображать в виде матрицы расстояний, где строки и столбцы представляют вершины графа, а элемент, стоящий на месте (i, j) есть расстояние от вершины vi до вершины vj.
2. Найдем в матрице расстояний наибольшие значения по строкам. Минимальное из найденных наибольших значений называется радиусом, а наибольшее − диаметром.
3. Множество вершин находящихся на одинаковом расстоянии от вершины v называется ярусом вершины v.
Продолжение предыдущего примера. Матрица расстояний графа G
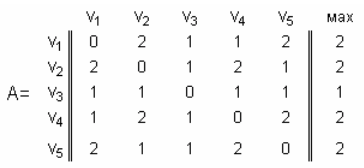
радиус (G) = min (max) = 1, диаметр (G) = mаx (max) = 2.