Две вершины в графе (орграфе) G называются смежными, если существует ребро (дуга), которая их соединяет. Пусть v, w вершины, а e = (v, w) − ребро (дуга) их соединяющая. Тогда вершина v и ребро (дуга) e являются инцидентными, вершина w и ребро (дуга) e также являются инцидентными. Два ребра инцидентные одной вершине называются смежными.

Пример. Рассмотрим неориентированный граф изображенный на рисунке:

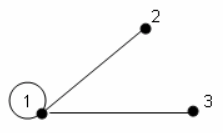
— Вершины 1,2 − смежные, а вершины 2,3 не являются смежными.

— Вершина 1 инцидентна ребру (1, 2). Ребро (2, 3) инцидентно вершине 2. Вершина 2 не инцидентна ребру (3, 1).

— Ребра (1, 2) и (1, 3) смежные, т.к. у них есть общая вершина.

Пример. Рассмотрим ориентированный граф изображенный на рисунке:

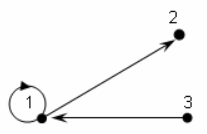
— Вершины 1, 2 − смежные, а вершины 2, 3 не являются смежными.

— Вершина 1 инцидентна дуге (1, 2). Дуга (3, 1) инцидентна вершине 1.

— Вершина 2 не инцидентна дуге (3, 1).

Степенью вершины v неориентированного графа G называется число δ(v) ребер инцидентных v. Вершина графа, имеющая степень 0, называется изолированной, а вершина степени 1 называется висячей.

Полустепенью исхода вершины v орграфа G называется число δ⁻(v) дуг исходящих из вершины v (т.е. v является началом этих дуг).

Полустепенью захода вершины v орграфа G называется число δ⁺(v) дуг входящих в вершину v (т.е. v является концом этих дуг).

Замечание. В случае неориентированного псевдографа вклад каждой петли при расчете степени инцидентной вершины равен 2.

Пример. Рассмотрим ориентированный псевдограф, изображенный на рисунке:

δ⁻(1) = 2, δ⁺(1) = 2, δ⁻(2) = 0, δ⁺(2) = 1, δ⁻(3) = 1, δ⁺(3) = 2.

Пример. Рассмотрим неориентированный псевдограф, изображенный на рисунке:

δ(1) = 4, δ(2) = 1, δ(3) = 1.

Утверждение. Пусть G граф с n вершинами и q ребрами. Тогда $\sum _{i=1}^n\sigma \left(i\right)=2q$ , где δ(i) − степень вершины i. Для доказательства утверждения, достаточно заметить, что каждое ребро дает в сумму вклад равный двум, т.к. соединяет ровно две вершины.

Следствие (лемма о рукопожатиях). В любом графе число вершин нечетной степени четно.

Утверждение. Пусть G орграф с n вершинами и q дугами. Тогда $\sum _{i=1}^n{\sigma }^{—}\left(i\right)=\sum _{i=1}^n{\sigma }^{+}\left(i\right)=q$ , где δ⁺(i), δ^—(i), − полустепени вершины i.