Графом G (в широком понимании) называется любая пара (V, E), где V = {v₁, v₂, …, v_n} – конечное множество элементов любой природы, а E = {e₁, e₂, …, e_m} — семейство пар элементов из V, причем допускаются пары вида (v_i, v_i) и одинаковые пары. Если пары в V рассматриваются как неупорядоченные, то граф называется неориентированным, если как упорядоченные, то граф называется ориентированным (орграфом). Элементы множества V называются вершинами графа, а пары из E − его ребрами; в орграфе они называются ориентированными ребрами или дугами. Пара вида (v_i, v_i) называется петлей в вершине v_i. Если пара (v_i, v_j) встречается в E более одного раза, то говорят, что (v_i, v_j) – кратное ребро. Говорят, что ребро e = (u, v) в неориентированном графе соединяет вершины u и v, а в ориентированном графе дуга e = (u, v) идет из вершины u в вершину v.

Дадим понятие графа в узком смысле, которое в основном и будем использовать в дальнейшем.

Определения.

1. Граф (в широком понимании) с петлями и возможно с кратными ребрами называют псевдографом (псевдоорграфом).

2. Граф (в широком понимании) с кратными ребрами, но без петель называют мультиграфом (мультиорграфом).

3. Графом (орграфом) называется граф (в широком понимании) без петель и кратных ребер.

Графы (орграфы) можно графически изображать следующим образом. Вершины будем изображать точками, а каждое ребро (дугу) (v i ,v j ) — линией, соединяющей точки v_i и v_j. Если (v_i, v_j) — дуга, то на этой линии будем указывать стрелку от v_i к v_j.

Примеры.

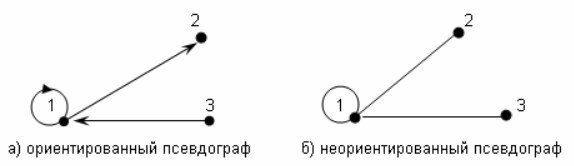
1. Псевдографы (в вершине 1 − петля).

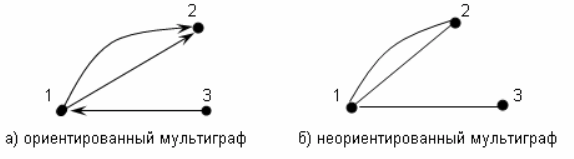
2. Мультиграфы (из вершины 1 идут две дуги/ребра в вершину 2).

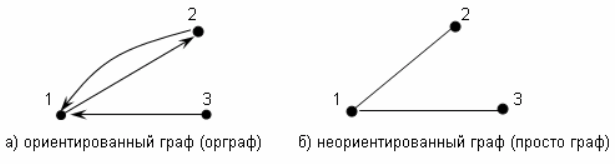
3. Графы (нет петель и кратных ребер/дуг: дуги (1, 2) и (2, 1) в орграфе считаются разными).

Ориентированный псевдограф на рисунке в примере 1.а аналитически задается следующим образом: G = (V, E), где V = {1, 2, 3}, E = {(1, 1), (1, 2), (3, 1)}.

Неориентированный псевдограф на рисунке в примере 1.б аналитически задается следующим образом: G = (V, E), где V = {1, 2, 3}, E = {(1, 1), (1, 2), (1, 3)} или V = {1, 2, 3}, E = {(1, 1), (2, 1), (1, 3)}, т.к. в неупорядоченной паре (2, 1) = (1, 2).

Ориентированный мультиграф на рисунке в примере 2.а аналитически задается следующим образом: G = (V, E), где V = {1, 2, 3}, E = {(1, 1), (1, 2), (1, 2), (3, 1)}.