Алгоритм 1. Поиск узла в дереве сортировки.

Вход: дерево сортировки T, заданное указателем t на корень; ключ a.

Выход: указатель p на найденный узел или nul, если в дереве нет такого ключа.

Этот алгоритм работает в точном соответствии с определением дерева сортировки. Если текущий узел не искомый, то в зависимости от того, меньше или больше искомый ключ по сравнению с текущим ключом, нужно продолжать поиск соответственно слева или справа.

Алгоритм 2. Вставка узла в дерево сортировки.

Вход: дерево сортировки Т, заданное указателем t на корень; ключ a.

Выход: модифицированное дерево сортировки Т.

Алгоритм вставки, в сущности, аналогичен алгоритму поиска: в дереве ищется такой узел, имеющий свободную связь для подцепления нового узла, чтобы не нарушалось условие дерева сортировки. А именно, если новый ключ меньше текущего, то либо его можно подцепить слева (если левая связь свободна), либо нужно найти слева подходящее место. Аналогично, если новый ключ больше текущего.

Алгоритм 3. Удаления из дерева сортировки.

Удаление узла производится перестройкой дерева сортировки. При этом возможны три случая (не считая тривиального случая, когда удаляемого узла нет в дереве и ничего делать не нужно).

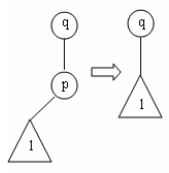
1. Правая связь удаляемого узла p пуста (см. рисунок ниже). В этом случае левое поддерево 1 узла p подцепляется к родительскому узлу q с той же стороны, с которой был подцеплен узел р. Условие дерева сортировки, очевидно, выполняется.

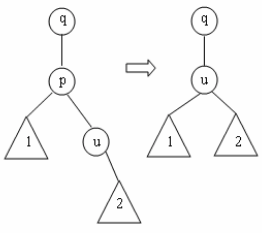
2. Правая связь удаляемого узла р не пуста и ведет в узел u, левая связь которого пуста (см. рисунок ниже). В этом случае левое поддерево 1 узла р подцепляется к узлу u слева, а сам узел u подцепляется к родительскому узлу q с той же стороны, с которой был подцеплен узел р. Нетрудно проверить, что условие дерева сортировки выполняется и в этом случае.

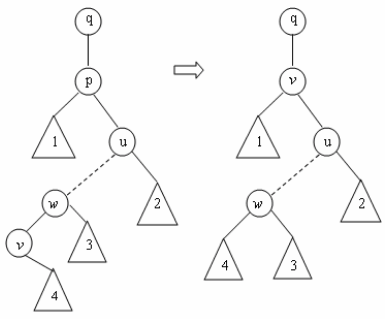
3. Правая связь удаляемого узла р не пуста и ведет в узел u, левая связь которого не пуста. Поскольку дерево сортировки конечно, можно спуститься от узла u до узла v, левая связь которого пуста (см. рисунок ниже). В этом случае выполняются два преобразования дерева. Сначала информация в узле р заменяется на информацию узла v. Поскольку узел v находится в правом поддереве узла р и в левом поддереве узла u, имеем p.i < v.i < u.i. Таким образом, после этого преобразования условие дерева сортировки выполняется. Далее правое поддерево 4 узла v подцепляется слева к узлу w, а сам узел v удаляется. Поскольку поддерево 4 входило в левое поддерево узла w, условие дерева сортировки также сохраняется.

Обычно дерево сортировки строится сразу упорядоченным.

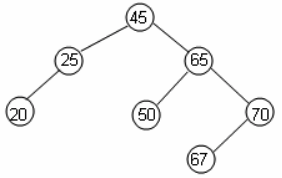
Пример 1. Пусть программа обработки данных составлена в соответствии с алгоритмами дерева сортировки. Для простоты предположим, что информационное поле совпадает с ключами. Постройте дерево сортировки по последовательности 45, 25, 60, 70, 15, 65, 20, 67.

Решением является следующее дерево сортировки:

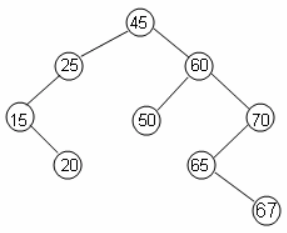
Пример 2. Удалим узлы 60 и 15 из решения примера 1: