Говорят, что две вершины u, v в графе G связаны отношением достижимости, если существует соединяющая их цепь <u, v>. Граф, в котором все вершины достижимы, называется связным. Тривиальный граф, состоящий из изолированной вершины, по определению считается связным. Приведем следующее очевидное утверждение.

Утверждение. Отношение достижимости вершин является отношением эквивалентности.

Компонентой связности графа G называется его связный подграф, который не является собственным подграфом никакого другого связного подграфа графа G.

Из предыдущего утверждения следует, что классы эквивалентности по отношению достижимости, являются разбиением множества вершин графа G, на подмножества вершин входящих в одну компоненту связности. Для построения компоненты связности достаточно взять один класс эквивалентности (вершин) и перенести на множество его вершин связи (ребра) из графа G.

Число компонент связности графа G обозначим c(G). Очевидно, граф G является связным тогда и только тогда, когда c(G) = 1. Если c(G) > 1, то G — несвязный граф. Граф, состоящий только из изолированных вершин, называется вполне несвязным.

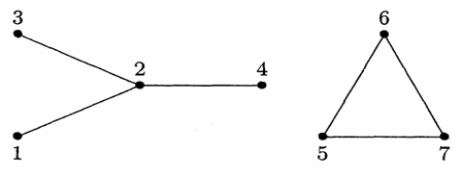
Пример. Граф, показанный на рисунке ниже, имеет две компоненты связности с множеством вершин V1 = {1, 2, 3, 4} и V2 = {5, 6, 7}.