Упорядоченное дерево T — это конечное множество узлов, таких что:
1. имеется один узел r, называемый корнем данного дерева;
2. остальные узлы (исключая корень) содержатся в k попарно непересекающихся множествах T1, T2, …, Tk, каждое из которых является ордеревом (множества T1, T2, …, Tk являются поддеревьями);
3. относительный порядок поддеревьев T1, T2, …, Tk фиксирован.
Другими словами, упорядоченное дерево T это ордерево, в котором множество сыновей каждого узла упорядочено. Порядок, как правило, устанавливается слева на право (и сверху вниз) по старшинству.
Исходя из определения, упорядоченное дерево обозначается в виде T = {r, T1, T2, …, Tk}.
Покажем на примере, как изображаются упорядоченные деревья графически.
Пример. Упорядоченные ориентированные деревья используются:
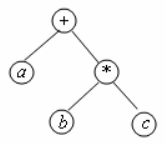
1. Для представления выражений языков программирования. Пример представления выражения a + b ∗ c показан на рисунке ниже. Отметим, что если, например, операция «∗» не обладает свойством коммутативности, то вершины «b» и «c» переставлять местами нельзя, иначе результат вычисления не будет соответствовать данному выражению. Поэтому данный граф является упорядоченным.
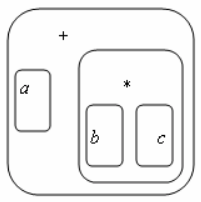
2. Для представления блочной структуры программы, часто используется ориентированное дерево (может быть, неупорядоченное, так, как порядок определения переменных в блоке в большинстве языков программирования считается несущественным). На рисунке ниже в центре показана структура областей определения выражения a + b ∗ c, причем для отображения структуры дерева использована альтернативная техника.
3. Для представления иерархической структуры вложенности элементов данных и/или операторов управления часто используется техника отступов, показанная на рисунке ниже.
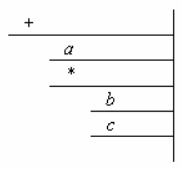
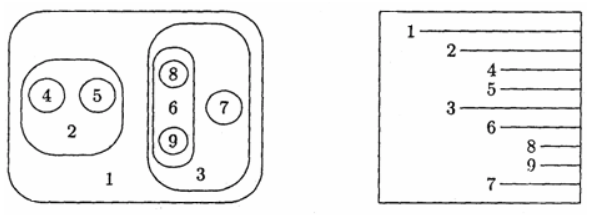
Пример. Пусть задано упорядоченное дерево (1, (2, (4), (5)), (3, (6, (8), (9)), (7))). Здесь r = 1, T1 = (2, (4), (5)), T2 = (3, (6, (8), (9)), (7)). Данному упорядоченному дереву соответствует система множеств, изображенная на рисунке ниже слева, и уступчатый список изображенный на рисунке справа. Из данного изображения видно, что объекты 2 и 3 являются братьями, причем объект 3 старше 2, т.к. расположен правее (на графе вершина 3 будет также расположена правее вершины 2). Для удобства, внутри блока старшинство можно считать определено сверху вниз (левый рисунок).
Согласно следующему тезису любая схема, в которой заданы определенные приоритеты между элементами, например, схема подчиненности на предприятии, может рассматриваться как некоторое упорядоченное дерево.
Тезис. Любая иерархическая классификационная схема описывается некоторым упорядоченным деревом.
Пример. Иерархическая система подчиненности на предприятии является упорядоченным деревом.
Замечание. Общепринятой практикой при изображении деревьев является соглашение о том, что корень находится наверху и все стрелки дуг ориентированы сверху вниз, поэтому стрелки можно не изображать. Таким образом, диаграммы свободных, ориентированных и упорядоченных деревьев оказываются графически неотличимыми, и требуется дополнительное указание, дерево какого класса изображено на диаграмме. В большинстве случаев это ясно из контекста.
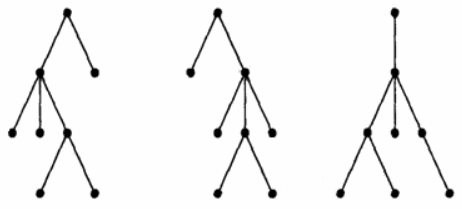
Пример. На рисунке ниже приведены три диаграммы деревьев, которые внешне выглядят различными. Обозначим дерево слева — (1), в центре — (2) и справа — (3). Как упорядоченные деревья, они все различны: (1) ≠ (2), (2) ≠ (3), (3) ≠ (1) (значок означает «не изоморфно»). Как ориентированные деревья (1) = (2), но (2) ≠ (3). Как свободные деревья, они все изоморфны: (1) = (2) = (3).