Обход графа — это некоторое систематическое перечисление его вершин (и/или ребер). Наибольший интерес представляют обходы, использующие локальную информацию (списки смежности). Среди всех обходов наиболее известны поиск в ширину и в глубину.

Алгоритмы поиска в ширину и в глубину лежат в основе многих конкретных алгоритмов на графах:

Если T − это стек (LIFO — Last In First Out), то обход называется поиском в глубину. Если T — это очередь (FIFO — First In First Out), то обход называется поиском в ширину.

Пример. В следующей таблице показаны протоколы поиска в глубину и в ширину для графа, диаграмма которого приведена на рисунке. Слева в таблице протокол поиска в глубину, а справа — в ширину. Предполагается, что начальной является вершина 1.

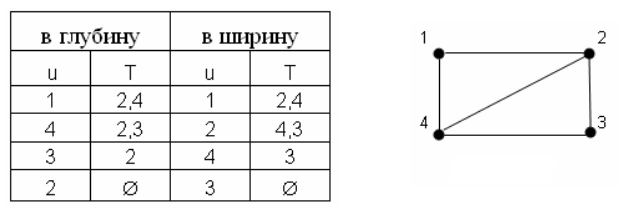
Теорема. Если граф G связен (и конечен), то поиск в ширину и поиск в глубину обойдут все вершины по одному разу.

Доказательство.

1. Единственность обхода вершины. Обходятся только вершины, попавшие в T. В T попадают только не отмеченные вершины. При попадании в T вершина отмечается. Следовательно, любая вершина будет обойдена не более одного раза.

2. Завершаемость алгоритма. Всего в Т может попасть не более р вершин. На каждом шаге одна вершина удаляется из T. Следовательно, алгоритм завершит работу не более чем через р шагов.

3. Обход всех вершин. От противного. Пусть алгоритм закончил работу, и вершина w не обойдена. Значит, w не попала в T. Следовательно, она не была отмечена. Отсюда следует, что все вершины, смежные с w, не были обойдены и отмечены. Аналогично, любые вершины, смежные с неотмеченными вершинами, сами не отмечены (после завершения алгоритма). Но G связен, значит, существует путь из v в w. Следовательно, вершина v не отмечена. Но она была отмечена на первом шаге. Противоречие.

Замечание. При поиске в ширину, вершины обходятся в порядке возрастания расстояния от начальной вершины (отсюда и название − поиск в ширину).