Говорят, что два графа G1(V1, E1) и G(V2, E2) изоморфны (обозначается G1~G2), если существует биекция h:V1→V2, сохраняющая смежность: (a, b) ∈ E1 — ребро графа G1 ⇔ (h(a), h(b)) ∈ E2 — ребро графа G2.
Утверждение. Изоморфизм графов есть отношение эквивалентности.
Действительно, изоморфизм обладает всеми необходимыми свойствами:
1. рефлексивность: G ~ G, где требуемую биекцию устанавливает тождественная функция;
2. симметричность: если G1 ~ G2 с биекцией h, то G2 ~ G1 с биекцией h−1;
3. транзитивность: если G1 ~ G2 с биекцией h и G2 ~ G3 с биекцией g, то G1 ~ G3 с биекцией h°g, являющейся композицией h и g.
Замечание 1. Из определения изоморфизма графов следует, что диаграммы изоморфных графов (орграфов) отличаются лишь обозначением вершин и их расположением на плоскости.
Замечание 2. Графы рассматриваются с точностью до изоморфизма, то есть рассматриваются классы эквивалентности по отношению изоморфизма.
Утверждение. У изоморфных графов одинаково:
• число вершин;
• число ребер;
• число вершин одинаковой степени (полустепени).
Пример. Три внешне различные диаграммы, приведенные на рисунке ниже, являются диаграммами одного и того же графа K3, 3. Действительно, если вершины графа G1 переобозначить так — v1 на u1, v2 на u2, …, v6 на u6, затем расположить в местах, где расположены вершины графа G2, потом восстановить связи (ребра) как в первом графе, то получится граф G2.

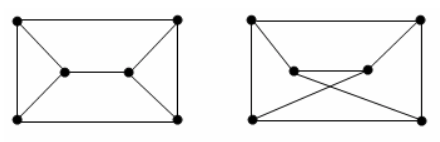
Замечание 3. Количество вершин, ребер и количество смежных вершин для каждой вершины не определяют граф. На рисунке ниже представлены диаграммы графов, у которых указанные инварианты совпадают, но графы при этом не изоморфны.