Пусть G(V, Е) — граф. Остовной подграф графа G(V, Е) — это подграф, содержащий все вершины. Остовный подграф, являющийся деревом, называется остовом. Очевидно, что несвязный граф не имеет остова. Связный граф может иметь много остовов.

Если задать длины ребер, то можно поставить задачу нахождения кратчайшего остова. Эта задача имеет множество практических интерпретаций. Например, пусть задано множество аэродромов и нужно определить минимальный (по сумме расстояний) набор авиарейсов, который позволил бы перелететь с любого аэродрома на любой другой. Решением этой задачи будет кратчайший остов полного графа расстояний между аэродромами.

Алгоритм, решающий задачу нахождения остова минимального веса во взвешенном графе G(V, Е), заключается в следующем:

1. Строим граф T(1), состоящий из множества вершин V и единственного ребра e(i), которое имеет минимальный вес.

2. Если граф Т(k) уже построен и k < n - 1, где n = |V|, то строим граф T(k + 1), добавляя к множеству ребер графа T(k) ребро e(i + 1) имеющее минимальный вес среди ребер, не входящих в T(k) и не составляющих циклов с ребрами из Т(k).

Приведенный алгоритм, в частности, позволяет находить остов в невзвешенном графе, положив для всех ребер вес равный 1.

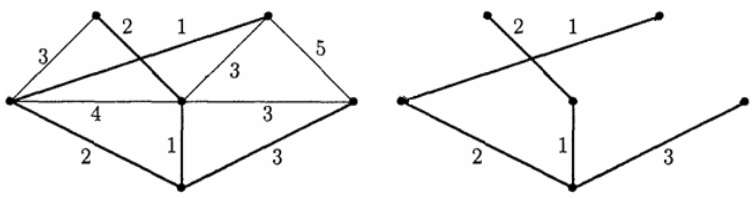
Пример. На рисунке ниже показан остов минимального веса взвешенного графа. Вес остова равен 9.