Пусть G = (V, E) граф (орграф) с n вершинами и q ребрами, т.е. V = {v1, v2, …, vn}, E = {e1, e2, …, eq}.
Следующая теорема позволяет по матрице смежности A(G) исследовать маршруты данного графа (орграфа) G.
Теорема. Если A = A(G) — матрица смежности графа (орграфа) G, то aij элемент матрицы Аk есть число маршрутов из vi в vj длины k.
Следствие. В n вершинном графе (орграфе) G тогда и только тогда существует маршрут из vi в vj (i ≠ j), когда (i, j)-й элемент матрицы A + A2 + … + An — 1 не равен нулю.
Следствие. В n вершинном графе (орграфе) G тогда и только тогда существует цикл; содержащий вершину ai, когда (i, i)-й элемент матрицы A + A2 + … +An — 1 + An не равен нулю.
Образуем из матрицы B = E + A + A2 + … +An — 1 + An матрицу C = (cij) порядка n по следующему правилу:
| cij = { | 1, если bij ≠ 0 |
| 0, если bij = 0 |
где bij элементы матрицы B.
Матрица C называется матрицей связности, если G — неориентированный граф, и матрицей достижимости, если G — орграф. В графе G тогда и только тогда существует маршрут из vi в vj (i ≠ j) когда cij = 1. Таким образом, в матрице C содержится информация о существовании связей между различными элементами графа посредством маршрутов. Если G — связный неориентированный граф, то все элементы матрицы связности C равны единице. В общем случае матрица связности неориентированного графа является матрицей отношения эквивалентности, соответствующего разбиению множества вершин графа на компоненты связности.
Пусть Ct транспонированная матрица С. В случае неориентированного графа C = Ct, и является матрицей связности. В случае ориентированного графа Ct называется матрицей контрдостижимости, т.к. если (i, j)-й элемент матрицы C показывает наличие пути из vi в vj, то (i, j)-й элемент матрицы Ct показывает наличие обратного пути из vj в vi.
Матрицы достижимости и контрдостижимости можно использовать для нахождения сильных компонент орграфа. Рассмотрим матрицу S = C * Ct, где операция * означает поэлементное произведение матриц C и Ct. Элемент sij матрицы S равен 1 тогда и только тогда, когда вершины vi и vj взаимно достижимы, т. е. vj достижима из vi и vi достижима из vj. Следовательно, сильная компонента, содержащая вершину vi, состоит из элементов vj, для которых sij = 1.
Пример. Найти компоненту сильной связности орграфа G, изображенного на рисунке ниже, содержащую вершину 2.
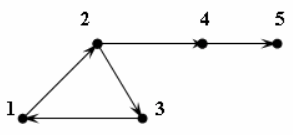
Решение. Матрицы достижимости C и контрдостижимости Ct орграфа, изображенного на предыдущем рисунке, имеют вид:



Из второй строки матрицы S находим, что сильная компонента, содержащая вершину 2, состоит из вершин {1, 2, 3}.