Граф называется взвешенным, если каждой вершине приписано некоторое математическое выражение называемое весом. Чтоб задать взвешенный граф достаточно задать матрицу весов W = (w_ij), где w_ij вес дуги (ребра) идущей из вершины v_i (i-я строка) в вершину v_j (j-й столбец). В данной главе мы считаем, что веса w_ij ∈ R, где R — множество действительных чисел, дополненное символом ∞.

Пусть G = {V, X} — взвешенный граф, имеющий п вершин и матрицу весов W = (w_ij), w_ij ∈ R. Опишем некоторые методы нахождения взвешенного расстояния от фиксированной вершины a_i ∈ V (называемой источником) до всех вершин графа G.

Мы будем предполагать, что в G отсутствуют контуры с отрицательным весом, поскольку, двигаясь по такому контуру достаточное число раз, то можно получить маршрут, имеющий вес, меньший любого заведомо взятого числа, и тем самым задача нахождения расстояния становится бессмысленной.

Алгоритм Форда-Беллмана.

1. Выбираем источник − вершину a_i.

2. Зададим строку D¹ = (d₁¹, d₂¹, …, d_n¹) − i-я строка в матрице W.

3. Последовательно определяем строки D^s = (d₁^s, d₂^s, …, d_n^s), где

d_j^s = min{d_j^s-1, d_k^s-1 + w_kj},

k = 1, 2, …, n,

j=1, 2, …, n.

Нетрудно видеть, что d_j^s — минимальный из весов маршрутов из a_i в a_j, состоящих не более чем из s дуг.

4. Искомая строка W — расстояний получается при s = n — 1.

Действительно, на этом шаге из весов всех маршрутов из a_i в a_j, содержащих не более n-1 дуг, выбирается наименьший, а каждый маршрут более чем с n-1 дугами содержит контур, добавление которого к маршруту не уменьшает w-расстояния, так как мы предположили отсутствие контуров отрицательного веса.

В обосновании алгоритма лежит принцип оптимальности Беллмана, который заключается в следующем: если в многошаговой задаче на каждом шаге применять оптимальный алгоритм, ведущий к оптимальному решению на данном шаге, то итоговый результат тоже будет оптимальным.

Замечание. Работу алгоритма можно завершить на шаге k, если D^k = D^k+1, т.к. посылки для получения D^k+2 будут такими же, как и при получении D^k+1 и, следовательно, D^k+1 = D^k+2.

Пример. Продемонстрируем работу алгоритма Форда-Беллмана на примере взвешенного графа, показанного на рисунке ниже, с матрицей весов W:

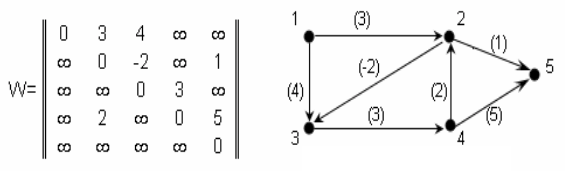
В качестве источника выберем вершину 1. Произведем вычисления по шагам.

1-шаг. D⁽¹⁾ = (0, 3, 4, ∞, ∞)

2-шаг. Вычислим D⁽²⁾. Согласно пункту 3) для вычисления d_j² надо взять вектор D⁽¹⁾ и сложить его покоординатно с j-ой строкой матрицы W, после чего найти минимум полученных координат и d_j¹:

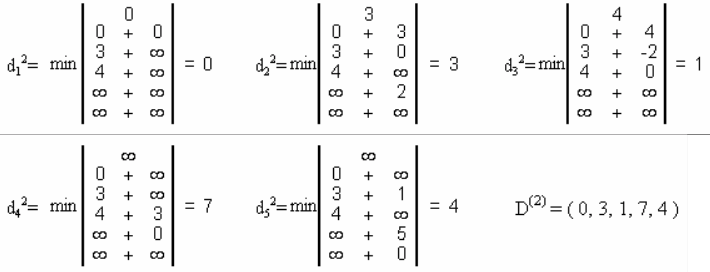
3-шаг. Так как D⁽²⁾ ≠ D⁽¹⁾, то вычисляем D⁽³⁾:

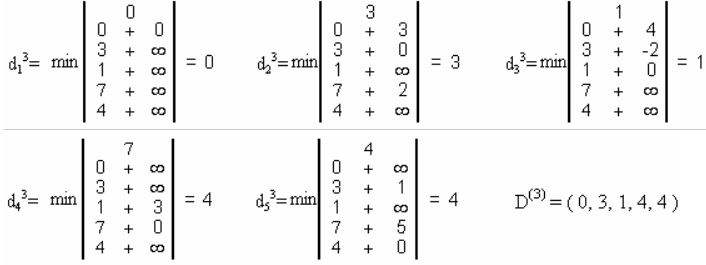
4-шаг. Так как D⁽³⁾ ≠ D⁽²⁾, то вычисляем D⁽⁴⁾:

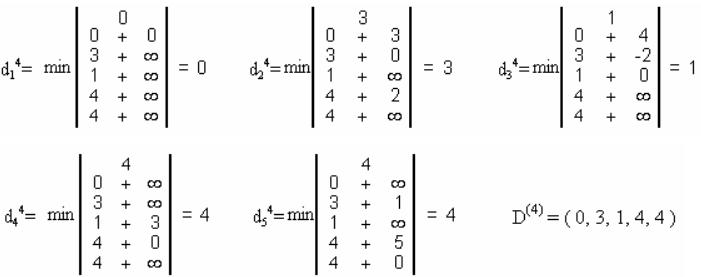
Вектор D⁽⁴⁾ определяет минимальные расстояния от источника 1 до вершин 1, 2, 3, 4, 5 соответственно.

Отметим, что, зная минимальное расстояние от источника a, до всех остальных вершин графа, можно восстановить минимальный маршрут по формуле:

ρ(a, b) = ρ(a, c) + w_cb, где

ρ(a, b) – минимальное расстояние от вершины a до вершины b.

Так, кратчайший (1, 4) — маршрут задается последовательностью вершин (1, 2, 3, 4), а кратчайший (1, 5) — маршрут задается последовательностью вершин (1, 3, 5).

Алгоритм Дейкстры является более эффективным, чем алгоритм Форда-Беллмана, но используется только для взвешенных графов, в которых веса всех дуг неотрицательны.

1. Выбираем источник − вершину a_i.

2. Зададим строку D¹ = (d₁¹, d₂¹, …, d_n¹) — i-я строка в матрице W. Обозначим T₁ = V \ {a_i}.

3. Предположим, что на шаге s уже определены строка D^s = (d₁^s, d₂^s, …, d_n^s) и множество вершин T_s.

4. Выбираем вершину a_j ∈ T_s такую, что d_j^s = min{d_k^s | a_k ∈ T_s}. Положим T_s+1 = T_s \ {a_j}, D^s+1 = (d₁^s+1, d₂^s+1, …, d_n^s+1), где d_k^s+1 = min{d_k^s, d_j^s + w_jk}, если a_k ∈ T_s+1, и d_k^s+1 = d_k^s, если a_k ∉ T_s+1.

5. На шаге s = n — 1 образуется строка D^n-1 w-расстояний между источником a_i; и остальными вершинами графа: d_k^n-1 = ρ(a_i, a_k).

Отметим, что для реализации алгоритма Форда-Беллмана требуется порядка n³ операций, тогда как в алгоритме Дейкстры необходимо выполнить порядка n² операций.

Пример. Рассмотрим взвешенный граф G с матрицей весов W и источником 1. Требуется найти кратчайшие расстояния от источника 1 до других вершин, используя алгоритм Дейкстры.

По алгоритму Дейкстры последовательно находим:

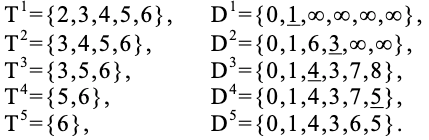
В D^s подчеркнута величина d_j^s, для которой T_s+1 = T_s \ {a_j}.

Отметим, что если в приведенных алгоритмах символ ∞ заменить на -∞, min на max, то получим алгоритмы, которые позволяют в графах, не имеющих контуров положительных весов, находить маршруты наибольшей длины.