Ориентированным деревом (или ордеревом, или корневым деревом) называется орграф со следующими свойствами:

1. существует единственный узел, полустепень захода которого равна 0. Он называется корнем ордерева;

2. полустепень захода всех остальных узлов равна 1;

3. каждый узел достижим из корня.

Пример. На рисунке ниже приведены диаграммы всех различных ориентированных деревьев с 3 и с 4 узлами:

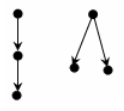
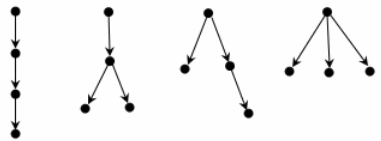
Теорема. Ордерево G(V, Е) с р вершинами и q дугами, обладает следующими свойствами:

1. q = p — 1;

2. если в ордереве отменить ориентацию ребер, то получится свободное дерево;

3. в ордереве нет контуров;

4. для каждого узла существует единственный путь, ведущий в этот узел из корня;

5. подграф, определяемый множеством узлов, достижимых из узла v, является ордеревом с корнем v (это ордерево называется поддеревом узла v);

6. если в свободном дереве любую вершину назначить корнем, то получится ордерево, при этом дуги будут последовательно ориентированы от корня обходом в глубину.

Концевая вершина (полустепень исхода равна 0) ордерева называется листом. Путь из корня в лист называется ветвью. Длина наибольшей ветви ордерева называется высотой. Уровень узла ордерева — это расстояние от корня до узла. Сам корень имеет уровень 0. Узлы одного уровня образуют ярус дерева.

Замечание. Наряду с «растительной» применяется еще и «генеалогическая» терминология. Узлы, достижимые из узла u, называются потомками узла u (потомки образуют поддерево). Если в дереве существует дуга (u, v), то узел u называется отцом (или родителем) узла v, а узел v называется сыном узла u. Сыновья одного узла называются братьями.