Граф, состоящий из одной вершины, называется тривиальным.
Граф, в котором каждая пара вершин смежна, называется полным. Другими словами, в полном графе каждая вершина, соединяется ребрами со всеми другими вершинами. Тривиальный граф по определению считается полным. Полный граф с p вершинами обозначается Kp, он имеет максимально возможное число ребер:

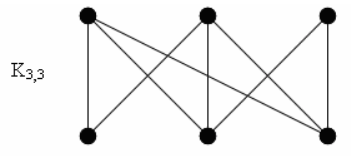
Двудольный граф (или биграф, или четный граф) — это граф G(V, E) у которого множество вершин V разбито на два непересекающихся множества V1 и V2 (т.е. V1∩V2 = ∅, V1∪V2 = V), причем всякое ребро из Е инцидентно вершине из V1 и вершине из V2 (то есть всякое ребро соединяет одну вершину из V1 с вершиной из V2). Множества V1 и V2 называются долями двудольного графа. Если в двудольном графе, каждая вершина из V1 соединяется ребрами со всеми вершинами из V2, то граф называется полным двудольным графом. Если |V1| = n, и |V2| = m, то полный двудольный граф обозначается Kn, m: