Пусть n — количество элементов в ассоциативной памяти, а h высота дерева (т.е. длина наибольшей цепи от корня до листа). Ордерево называется выровненным, если все узлы, степень которых меньше 2, располагаются на одном или двух последних уровнях. Выровненное дерево имеет наименьшую высоту из всех бинарных деревьев с количеством узлов n:

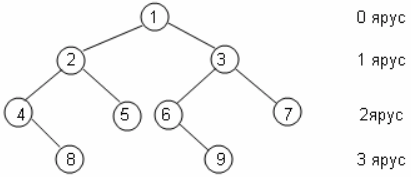
Теорема. Для выровненного дерева высота h удовлетворяет неравенству log₂(n + 1) − 1 ≤ h ≤ log₂(n + 1).

Доказательство. Сравним выровненное дерево, высота которого h, c выровненным деревом все листы которого находятся на одном ярусе h. Тогда количество вершин n ≤ 1 + 2 + 2² + 2³ + … + 2^h = 2^{h + 1} — 1. Откуда log₂(n + 1) — 1 ≤ h. Аналогично, сравним выровненное дерево высоты h, c выровненным деревом все листы находятся на одном ярусе h − 1. Получим n ≥ 1 + 2 + 2² + 2³ + … + 2^{h — 1} = 2^h − 1. Откуда h ≤ log₂(n + 1).

Сравним сложность операций (найти, добавить, удалить) для различных представлений ассоциативной памяти.

Для неупорядоченного массива операция добавить производится довольно легко и не зависит от числа элементов массива n − надо просто добавить элемент в конец массива. Сложность такой операции О(1). Однако, чтобы найти элемент (тоже и для операции удалить) в таком массиве необходимо организовать цикл от 1 до n, т.е. сложность такой операции О(n).

Для упорядоченного массива операция найти производится так: сравниваем значение ключа a искомого объекта с ключом элемента стоящего на месте [n / 2], если он меньше, то поиск продолжаем среди элементов находящихся на местах 1, 2, …, [n / 2] — 1, а если больше, то среди элементов [n / 2] + 1, [n / 2] + 2, …, n. Т.о. с каждым шагом мы уменьшаем число сравниваемых объектов в два раза. Теперь ясно, что сложность такой операции O(log₂(n)). Для операции добавить (и удалить) надо сначала найти место вставки, а затем произвести перенумерацию элементов ключи, которых больше a. Если мы вставляем элемент на место 1, то все элементы первоначального массива имеют новые индексы, начиная с 2 до n + 1. Сложность такой операции будет О(n).

При обходе выровненного дерева сортировки на каждом шаге мы отбрасываем где-то половину элементов, т.к. идем либо по левому, либо по правому поддереву. Поэтому, сложность операций найти, добавить, удалить составляет O(log₂(n)).

Отметим, что частным случаем дерева сортировки является упорядоченный массив (например, все элементы, поступающие на обработку, упорядочены по возрастанию ключей). Однако, эта ситуация при достаточно большом количестве узлов маловероятна. Обычно, деревья сортировки, по своей структуре занимают промежуточное положение между упорядоченным массивом и выровненным деревом сортировки. Поэтому, сложность операций найти, добавить, удалить составляет О(log₂(n)) … O(n).

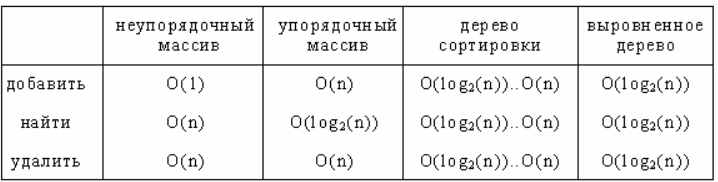
Сведем все сказанное в таблицу: сложность операций ограничена сверху значениями:

Пример. База данных состоит из 10⁶ (миллиона) записей. Сколько надо максимум обработать узлов, если ассоциативная память представлена выровненным деревом.

Ответ: Максимум 20 узлов, т.к. log₂(10⁶) = 19,93.

Пример. Ответить на вопрос предыдущего примера, если ассоциативная память представлена упорядоченным массивом.

Ответ: Максимум миллион узлов.

Пример. В базе данных, состоящей из 10⁶ (миллиона) записей, поиск нужной записи производился, максимум за 0,1 сек. База данных увеличилась в 1000 раз. Во сколько раз увеличится время обработки узлов, если ассоциативная память представлена выровненным деревом.

Ответ: Максимальное увеличение обхода узлов увеличилось с 20 узлов до 30 узлов, т.к. log₂(10⁹) = 29,90. Поэтому максимальное время обработки увеличится до 0,15 сек.

Пример. Допустим, что 100 узлов обрабатывается программой за 0,1 сек. Если структура данных представлена упорядоченным массивом и состоит из 10⁹ узлов, то какое максимальное время может потребоваться для поиска нужного узла.

Ответ. 10⁶ сек = 277,8 часов = 11,5 дней.