Вершины в графе часто называют узлами. Связный граф без циклов называется (свободным) деревом. Граф, компонентами связности которого являются деревья, называется лесом. Таким образом, лес состоит из нескольких деревьев.

Ниже на рисунке показаны диаграммы всех различных (свободных) деревьев с 5 вершинами:

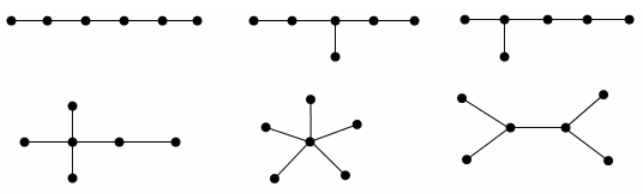
а на следующем рисунке — диаграммы всех различных (свободных) деревьев с 6 вершинами:

Теорема. Пусть G(V, Е) — граф с р вершинами, q ребрами.

Следующие утверждения эквивалентны:

1. G — дерево, то есть связный граф без циклов;

2. любые две вершины соединены в G единственной простой цепью;

3. G — связный граф, и любое ребро есть мост, т.е. его удаление делает граф не связным;

4. G — связный граф и q = p — 1;

5. G — связный граф и нет простых циклов.

Следствие. В любом дереве имеется, по крайней мере, две висячие вершины.