Пусть G = (V, E) ориентированный граф (орграф).
А) Сильная связность.
Говорят, что две вершины u, v в орграфе G связаны отношением двусторонней достижимости, если существует маршрут из u в v, а также маршрут из v в u. Орграф, в котором любые две вершины двусторонне достижимы, называется сильно связным. Тривиальный граф, состоящий из изолированной вершины, по определению считается сильно связным.
Утверждение. Отношение двусторонней достижимости вершин является отношением эквивалентности.
Компонентой сильной связности орграфа G называется его сильно связный подграф, который не является собственным подграфом никакого другого сильно связного подграфа орграфа G.
Из предыдущего утверждения следует, что классы эквивалентности по отношению двусторонней достижимости, являются разбиением множества вершин орграфа G на подмножества вершин, входящих в одну компоненту сильной связности. Для построения компоненты сильной связности достаточно взять один класс эквивалентности и перенести на множество его вершин связи (дуги) из орграфа G.
Число компонент сильной связности орграфа G обозначим k(G). Орграф G является сильно связным тогда и только тогда, когда k(G) = 1. Если k(G) > 1, то G — не является сильно связным орграфом.
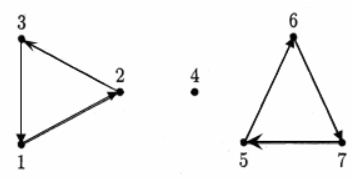
Пример. Граф, показанный на рисунке ниже не является сильно связным, т.к. имеет три компоненты сильной связности с множеством вершин V1 = {1, 2, 3}, V2 = {4} и V3 = {5, 6, 7}:

Сами компоненты сильной связности изображены на рисунке ниже:
Б) Односторонняя связность.
Орграф G называется односторонне связанным, если для любых двух вершин u, v существует маршрут хотя бы в одну сторону, т.е. либо маршрут из u в v, либо маршрут из v в u.
Очевидно, что если орграф является сильно связным, то он будет и односторонне связным.
Пример. Граф, показанный на рисунке ниже, не является односторонне связанным, т.к. скажем из вершины 1 нет пути в вершину 5 и наоборот, из вершины 5 нет пути в вершину 1:

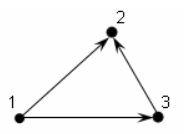
Пример. Граф на рисунке ниже, не является сильно связным, но является односторонне связным:
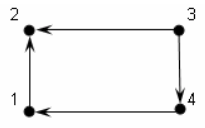
Пример. Граф на рисунке ниже, не является односторонне связным, т.к. для вершин 1 и 3 не существует пути <1, 3> и не существует пути <3, 1>:
В) Слабая связность.
Псевдографом ассоциированным с орграфом G = (V, E) называется псевдограф G1 = (V1, E1), в котором E1 получается из E заменой всех дуг (упорядоченных пар) на ребра (неупорядоченные пары).
Орграф G = (V, E) называется слабо связным, если ассоциированный с ним неориентированный граф является связным.
Пример. Граф изображенный на предыдущем рисунке, является слабо связным.